If (xa)+(yb)=1 and (xc)+(yd)=1 intersect the axes at four concylic points and a2+c2=b2+d2, then these lines can intersect at, (a,b,c,d>0)
(1,1)
(1,-1)
(2,-2)
(3,3)
The correct Answer is:A, B, C and D
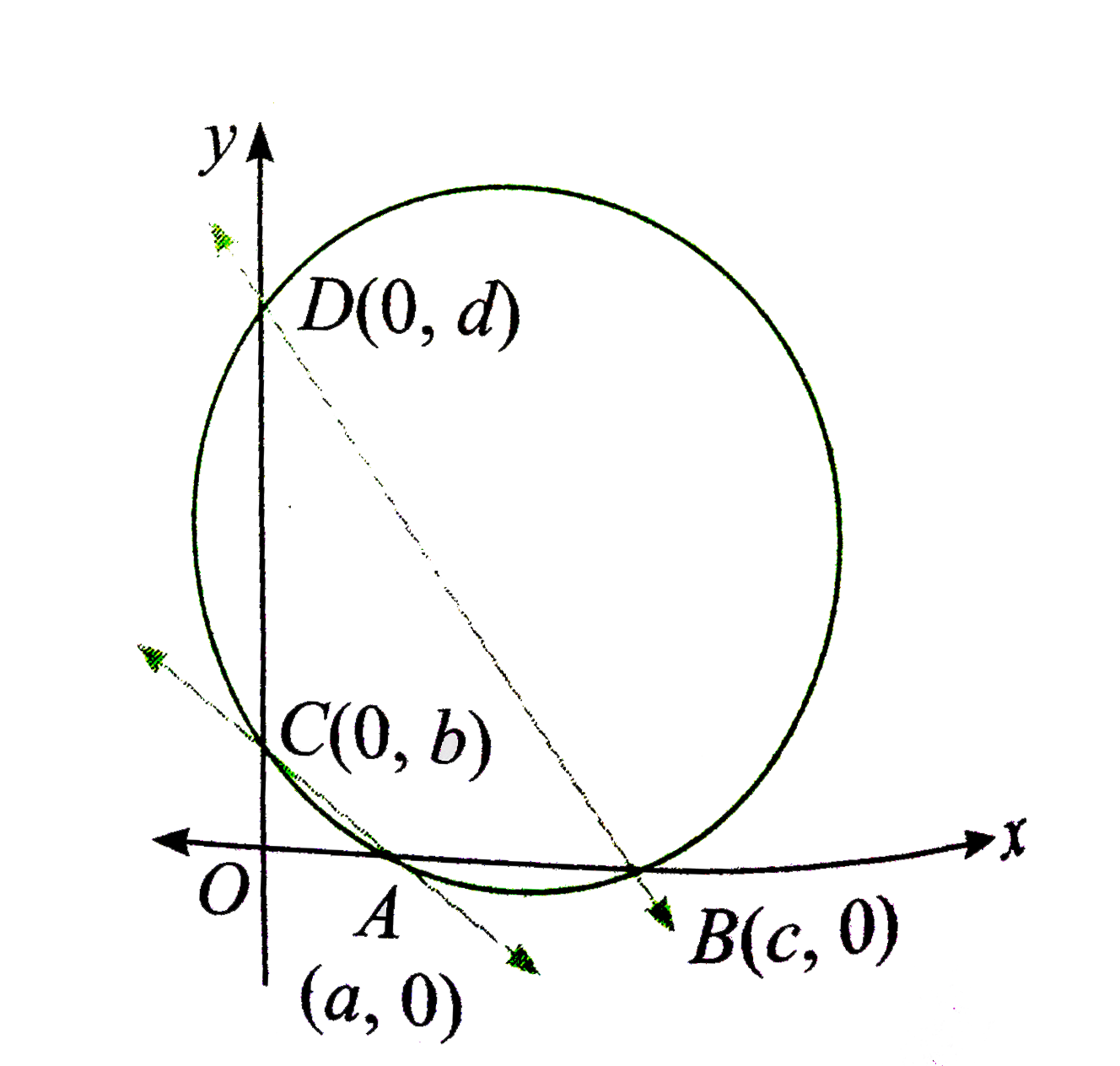
If points A, B,C,D are concyclic, then ac=bd. The coordinates of the points of intersection of lines are
(ac(b−d)bc−ad,bd(c−a)bc−ad)
Let the coordinates of the point of intersection be (h,k). Then
h=ac(b−d)bc−ad,k=bd(c−a)bc−ad
Given c2+a2=b2+d2.Since ac=bd, we have
(c−a)2=(b−d)2
or (c−a)=±(b−d)
Then the locus of the points of intersection is y=±x.
Topper's Solved these Questions
- STRAIGHT LINESBook:CENGAGE ENGLISHChapter:STRAIGHT LINESExercise:EXERCISE (LINKED COMPREHENSION TYPE)
Explore 27 Videos
- STRAIGHT LINESBook:CENGAGE ENGLISHChapter:STRAIGHT LINESExercise:EXERCISE (MATRIX MATCH TYPE)
Explore 8 Videos
- STRAIGHT LINESBook:CENGAGE ENGLISHChapter:STRAIGHT LINESExercise:EXERCISE (SINGLE CORRECT ANSWER TYPE)
Explore 82 Videos
- STRAIGHT LINEBook:CENGAGE ENGLISHChapter:STRAIGHT LINEExercise:Multiple Correct Answers Type
Explore 8 Videos
- THEORY OF EQUATIONSBook:CENGAGE ENGLISHChapter:THEORY OF EQUATIONSExercise:JEE ADVANCED (Numerical Value Type )
Explore 1 Video
Similar Questions
(x−1)(y−2)=5 and (x−1)2+(y+2)2=r2 intersect at four points A, B, C, D and if centroid of △ABC lies on line y=3x−4 , then locus of D is
View SolutionIf x2+y2=c2 and xa+yb=1 intersect at A and B, then find AB. Hence deduce the condition that the line touches the circle.
View SolutionThe ellipse x2a2+y2b2=1 and the straight line y=mx+c intersect in real points only if:
View SolutionIf the two intersecting lines intersect the hyperbola and neither of them is a tangent to it, then the number of intersecting points are (a)1 (b) 2 (c) 3 (d) 4
View SolutionSuppose a parabola y=x2−ax−1 intersects the coordinate axes at three points A,B and C, respectively. The circumcircle of ΔABC intersects the y-axis again at the point D(0,t). Then the value of t is
View SolutionIf the curves x2a2+y2b2=1andx2c2+y2d2=1 intersect orthogonally, then
View SolutionThe line x+2y=a intersects the circle x2+y2=4 at two distinct points AandB Another line 12x−6y−41=0 intersects the circle x2+y2−4x−2y+1=0 at two CandD. The value of 'a' for which the points A,B,CandD are concyclic -
View SolutionConsider two curves C1:y2=4x ; C2=x2+y2−6x+1=0. Then, a. C1 and C2 touch each other at one point b. C1 and C2 touch each other exactly at two point c. C1 and C2 intersect(but do not touch) at exactly two point d. C1 and C2 neither intersect nor touch each other
View SolutionThe lines 3x+4y=9&4x−3y+12=0 intersect at P. The first line intersects x−aξs at A and the second line intersects y−aξs at B. Then the circumradius of the triangle PAB is 32 (b) 52 (c) 10 (d) none
View SolutionIf the equations ax+by=1 and cx2+dy2=1 have only one solution, prove that a2c+b2d=1 and x=ac,y=bd
View Solution
