A(1, 1) and B(2,-3) are two points and D is a point on AB produced such that AD = 3AB. Find the co-ordinates of D.
We have ADAB=3
∴ADAD−AB=33−1
⇒ADBD=32
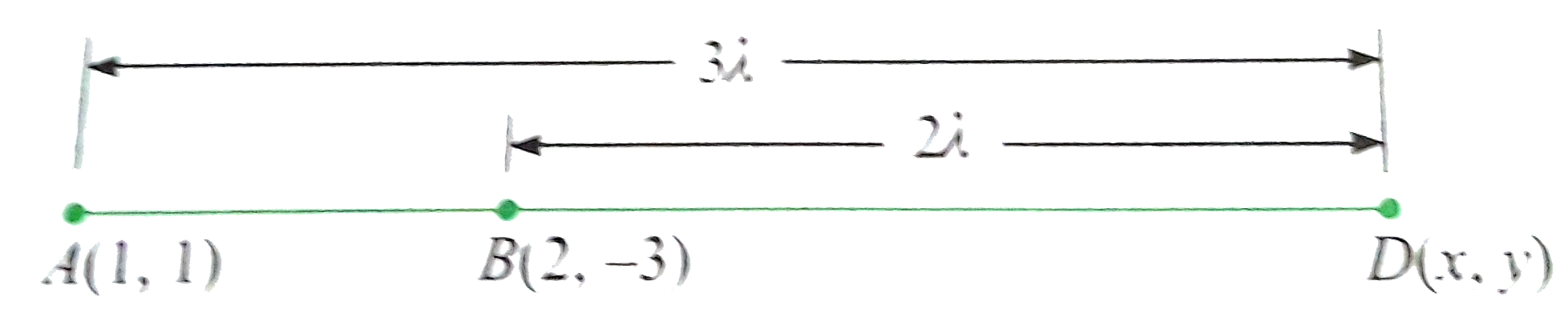
∴(x,y)≡(3(2)−2(1)3−2,3(−3)−2(1)3−2)≡(4,−11)
Topper's Solved these Questions
- BOOK - CENGAGE ENGLISHCHAPTER - COORDINATE SYSYEM EXERCISE - Illustration1.251videos
COORDINATE SYSYEM
- BOOK - CENGAGE ENGLISHCHAPTER - COORDINATE SYSYEM EXERCISE - Illustration1.261videos
COORDINATE SYSYEM
- BOOK - CENGAGE ENGLISHCHAPTER - COORDINATE SYSYEM EXERCISE - Illustration1.231videos
COORDINATE SYSYEM
- BOOK - CENGAGE ENGLISHCHAPTER - COORDINATE SYSTEMEXERCISE - Multiple Correct Answers Type2videos
COORDINATE SYSTEM
- BOOK - CENGAGE ENGLISHCHAPTER - CROSS PRODUCTS EXERCISE - DPP 2.213videos
CROSS PRODUCTS
Similar Questions
Given that A(1,1) and B(2,−3) are two points and D is a point on AB produced such that AD=3AB. Find the coordinates of D.
View SolutionLet A(2,−1,4) and B(0,2,−3) be the points and C be a point on AB produced such that 2AC=3AB, then the coordinates of C are
View SolutionA(1,4)andB(4,8) are two points. P is a point on AB such that AP=AB+BP. If AP=10, find the coordinates of P.
View SolutionIf D(3,-2) , E(-3,1) and F(4,-3) are the mid-points of the sides BC, CA and AB respectively of ΔABC , find the co-ordinates of point A , B and C .
View SolutionA straight line passes through the points A(-5, 2) and B(3,6). It intersects the co-ordinate axes at points C and D . M is a point on AB which divides CD in the ratio 1: 2. Find :
the co-ordinates of points C and D.View SolutionThe line joining the points A (-3, -10) and B (-2, 6) is divided by the point P such that PBAB=15. Find the co-ordinates of P.
View SolutionA straight line passes through the points A(-5, 2) and B(3,6). It intersects the co-ordinate axes at points C and D . M is a point on AB which divides CD in the ratio 1: 2. Find :
the co-ordinates of point M.View SolutionA is a point on x- axis, and point B (5,-4) and AB = 5 units find the co-ordinates of A.
View SolutionIf →a & →b are the position vectors of A & B respectively and C is a point on AB produced such that AC=3AB then the position vector of C is:
View SolutionA(20, 0) and B (10, -20) are two fixed points. Find the co-ordinates of the point P in AB such that : 3PB = AB. Also , find the co-ordinates of some other Point Q in AB such that : AB = 6 AQ.
View Solution

