A straight line passes through the points A(-5, 2) and B(3,6). It intersects the co-ordinate axes at points C and D . M is a point on AB which divides CD in the ratio 1: 2. Find :
the co-ordinates of point M.
The correct Answer is:M=(−2,−1)
To find the coordinates of point M that divides the line segment CD in the ratio 1:2, we first need to determine the coordinates of points C and D, where the line AB intersects the coordinate axes.
Step 1: Find the equation of the line passing through points A and B.
Given points:
- A(-5, 2) = (x1, y1)
- B(3, 6) = (x2, y2)
The slope (m) of the line through points A and B is given by:
m=y2−y1x2−x1=6−23−(−5)=48=12
Using the point-slope form of the line equation:
y−y1=m(x−x1)
Substituting the values:
y−2=12(x+5)
Step 2: Simplify the equation of the line.
Multiplying both sides by 2 to eliminate the fraction:
2(y−2)=x+5
2y−4=x+5
Rearranging gives:
x−2y+9=0
Step 3: Find the x-intercept (C) by setting y = 0.
Substituting y = 0 into the equation:
x−2(0)+9=0⟹x+9=0⟹x=−9
Thus, the coordinates of point C are:
C(−9,0)
Step 4: Find the y-intercept (D) by setting x = 0.
Substituting x = 0 into the equation:
0−2y+9=0⟹−2y+9=0⟹2y=9⟹y=92
Thus, the coordinates of point D are:
D(0,92)
Step 5: Use the section formula to find the coordinates of point M.
Point M divides the line segment CD in the ratio 1:2. Using the section formula:
M(mx2+nx1m+n,my2+ny1m+n)
where:
- C(x1,y1)=(−9,0)
- D(x2,y2)=(0,92)
- m=1, n=2
Substituting the values:
M⎛⎝1⋅0+2⋅(−9)1+2,1⋅92+2⋅01+2⎞⎠
Calculating the x-coordinate:
Mx=0−183=−183=−6
Calculating the y-coordinate:
My=92+03=923=96=32
Thus, the coordinates of point M are:
M(−6,32)
Final Answer:
The coordinates of point M are (−6,32).
---
- A(-5, 2) = (x1, y1)
- B(3, 6) = (x2, y2)
m=y2−y1x2−x1=6−23−(−5)=48=12
y−y1=m(x−x1)
Substituting the values:
y−2=12(x+5)
2(y−2)=x+5
2y−4=x+5
Rearranging gives:
x−2y+9=0
x−2(0)+9=0⟹x+9=0⟹x=−9
Thus, the coordinates of point C are:
C(−9,0)
0−2y+9=0⟹−2y+9=0⟹2y=9⟹y=92
Thus, the coordinates of point D are:
D(0,92)
M(mx2+nx1m+n,my2+ny1m+n)
where:
- C(x1,y1)=(−9,0)
- D(x2,y2)=(0,92)
- m=1, n=2
M⎛⎝1⋅0+2⋅(−9)1+2,1⋅92+2⋅01+2⎞⎠
Calculating the x-coordinate:
Mx=0−183=−183=−6
Calculating the y-coordinate:
My=92+03=923=96=32
M(−6,32)
The coordinates of point M are (−6,32).
Topper's Solved these Questions
Similar Questions
A straight line passes through the points A(-5, 2) and B(3,6). It intersects the co-ordinate axes at points C and D . M is a point on AB which divides CD in the ratio 1: 2. Find :
the co-ordinates of points C and D.
View SolutionA straight line passes through the points A(-5, 2) and B(3,-6). It intersects the co-ordinate axes at points C and D . Find :
the equation of AB.
View SolutionA straight line passes through the points P(-1, 4) and Q(5,-2). It intersects the co-ordinate axes at points A and B. M is the midpoint of the segment AB. Find :
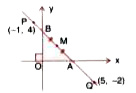
The equation of the line.
View SolutionA straight line passes through the points P(-1, 4) and Q(5,-2). It intersects the co-ordinate axes at points A and B. M is the midpoint of the segment AB. Find :
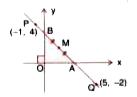
The co-ordinates of M.
View SolutionA straight line passes through the points P(-1, 4) and Q(5,-2). It intersects the co-ordinate axes at points A and B. M is the midpoint of the segment AB. Find :
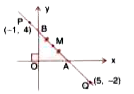
The co-ordinates of A and B.
View SolutionA straight line passes through the points P(−1,4) and Q(5,−2). It intersects x-axis at point A and y-axis at point B. M is the midpoint of the line segment AB. Find :
the co-ordinates of point M.
View SolutionFind the equation of a plane passes through the point (1,2,3) and cuts equal intercepts on the co-ordinate axes.
View SolutionThe equation of the straight line passing through the point (4.3) and making intercepts on the co ordinate axes whose sum is −1, is
View SolutionThe equation of the straight line passing through the point (4.3) and making intercepts on the co ordinate axes whose sum is −1, is
View SolutionA(1, 1) and B(2,-3) are two points and D is a point on AB produced such that AD = 3AB. Find the co-ordinates of D.
View Solution
