A straight line passes through the points A(-5, 2) and B(3,6). It intersects the co-ordinate axes at points C and D . M is a point on AB which divides CD in the ratio 1: 2. Find :
the co-ordinates of points C and D.
The correct Answer is:C=(−3,0)andD=(0,−3)
To find the coordinates of points C and D where the line passing through points A(-5, 2) and B(3, 6) intersects the coordinate axes, we will follow these steps:
Step 1: Find the equation of the line passing through points A and B.
The formula for the equation of a line in two-point form is given by:
y−y1y2−y1=x−x1x2−x1
Here, we have:
- A(x1,y1)=(−5,2)
- B(x2,y2)=(3,6)
Substituting the values into the formula:
y−26−2=x+53−(−5)
This simplifies to:
y−24=x+58
Step 2: Cross-multiply to eliminate the fractions.
Cross-multiplying gives us:
8(y−2)=4(x+5)
Expanding both sides:
8y−16=4x+20
Step 3: Rearranging to standard form.
Rearranging the equation to standard form:
4x−8y+36=0
This can be simplified to:
x−2y+9=0
Step 4: Find the coordinates of point C (where the line intersects the x-axis).
To find point C, we set y=0:
x−2(0)+9=0
This simplifies to:
x+9=0⟹x=−9
Thus, the coordinates of point C are:
C(−9,0)
Step 5: Find the coordinates of point D (where the line intersects the y-axis).
To find point D, we set x=0:
0−2y+9=0
This simplifies to:
−2y+9=0⟹2y=9⟹y=92
Thus, the coordinates of point D are:
D(0,92)
Final Answer:
The coordinates of points C and D are:
- C: (-9, 0)
- D: (0, 4.5)
- A(x1,y1)=(−5,2)
- B(x2,y2)=(3,6)
- C: (-9, 0)
- D: (0, 4.5)
Topper's Solved these Questions
Similar Questions
A straight line passes through the points A(-5, 2) and B(3,6). It intersects the co-ordinate axes at points C and D . M is a point on AB which divides CD in the ratio 1: 2. Find :
the co-ordinates of point M.View SolutionA straight line passes through the points A(-5, 2) and B(3,-6). It intersects the co-ordinate axes at points C and D . Find :
the equation of AB.View SolutionA straight line passes through the points P(-1, 4) and Q(5,-2). It intersects the co-ordinate axes at points A and B. M is the midpoint of the segment AB. Find :

The equation of the line.View SolutionA straight line passes through the points P(-1, 4) and Q(5,-2). It intersects the co-ordinate axes at points A and B. M is the midpoint of the segment AB. Find :
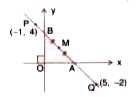
The co-ordinates of M.View SolutionA straight line passes through the points P(-1, 4) and Q(5,-2). It intersects the co-ordinate axes at points A and B. M is the midpoint of the segment AB. Find :
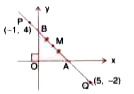
The co-ordinates of A and B.View SolutionA straight line passes through the points P(−1,4) and Q(5,−2). It intersects x-axis at point A and y-axis at point B. M is the midpoint of the line segment AB. Find :
the co-ordinates of point M.View SolutionFind the equation of a plane passes through the point (1,2,3) and cuts equal intercepts on the co-ordinate axes.
View SolutionA(1, 1) and B(2,-3) are two points and D is a point on AB produced such that AD = 3AB. Find the co-ordinates of D.
View SolutionThe equation of the straight line passing through the point (4.3) and making intercepts on the co ordinate axes whose sum is −1, is
View SolutionThe equation of the straight line passing through the point (4.3) and making intercepts on the co ordinate axes whose sum is −1, is
View Solution

