In triangle ABC< D is on AC such that AD=BC and BD=DC, ∠DBC=2x and ∠BAD=3x where each angle is in degree. Then find x
To solve the problem step by step, let's break it down:
Given:
- Triangle ABC with point D on AC such that:
- AD=BC
- BD=DC
- Angles:
- ∠DBC=2x
- ∠BAD=3x
To Find:
- The value of x.
Step 1: Identify Angles in Triangle DBC
Since AD=BC, by the property of isosceles triangles, the angles opposite these sides are equal. Therefore:
- ∠DBA=∠BAD=3x
Step 2: Identify Angles in Triangle BDC
Since BD=DC, again by the property of isosceles triangles:
- ∠DCB=∠DBC=2x
Step 3: Apply the Triangle Sum Property in Triangle DBC
The sum of angles in triangle DBC is equal to 180 degrees:
∠DBC+∠DCB+∠BDC=180∘
Substituting the known values:
2x+2x+∠BDC=180∘
This simplifies to:
4x+∠BDC=180∘
Thus, we can express ∠BDC as:
∠BDC=180∘−4x
Step 4: Use the Linear Pair Property
Angles ∠ADB and ∠BDC form a linear pair, so:
∠ADB+∠BDC=180∘
Substituting ∠BDC:
∠ADB+(180∘−4x)=180∘
This implies:
∠ADB=4x
Step 5: Apply the Triangle Sum Property in Triangle ABD
Now, we can apply the triangle sum property in triangle ABD:
∠DAB+∠ADB+∠ABD=180∘
Substituting the known values:
3x+4x+3x=180∘
This simplifies to:
10x=180∘
Step 6: Solve for x
Dividing both sides by 10:
x=180∘10=18∘
Final Answer:
The value of x is 18∘.
---
- Triangle ABC with point D on AC such that:
- AD=BC
- BD=DC
- Angles:
- ∠DBC=2x
- ∠BAD=3x
- The value of x.
Since AD=BC, by the property of isosceles triangles, the angles opposite these sides are equal. Therefore:
- ∠DBA=∠BAD=3x
Since BD=DC, again by the property of isosceles triangles:
- ∠DCB=∠DBC=2x
The sum of angles in triangle DBC is equal to 180 degrees:
∠DBC+∠DCB+∠BDC=180∘
Substituting the known values:
2x+2x+∠BDC=180∘
This simplifies to:
4x+∠BDC=180∘
Thus, we can express ∠BDC as:
∠BDC=180∘−4x
Angles ∠ADB and ∠BDC form a linear pair, so:
∠ADB+∠BDC=180∘
Substituting ∠BDC:
∠ADB+(180∘−4x)=180∘
This implies:
∠ADB=4x
Now, we can apply the triangle sum property in triangle ABD:
∠DAB+∠ADB+∠ABD=180∘
Substituting the known values:
3x+4x+3x=180∘
This simplifies to:
10x=180∘
Dividing both sides by 10:
x=180∘10=18∘
The value of x is 18∘.
Topper's Solved these Questions
- PROPERTIES AND SOLUTIONS OF TRIANGLEBOOK - CENGAGE ENGLISHCHAPTER - PROPERTIES AND SOLUTIONS OF TRIANGLEEXERCISE - Illustration
86 Videos
- PROPERTIES AND SOLUTIONS OF TRIANGLEBOOK - CENGAGE ENGLISHCHAPTER - PROPERTIES AND SOLUTIONS OF TRIANGLEEXERCISE - Concept application exercise 5.1
12 Videos
- PROGRESSION AND SERIESBOOK - CENGAGE ENGLISHCHAPTER - PROGRESSION AND SERIESEXERCISE - ARCHIVES (MATRIX MATCH TYPE )
1 Videos
- RELATIONS AND FUNCTIONSBOOK - CENGAGE ENGLISHCHAPTER - RELATIONS AND FUNCTIONSEXERCISE - Archives(Matrix Match Type)
1 Videos
Similar Questions
Given △ABC~△PQR if ABPQ=13 then find ar△ABCar△PQR
View SolutionIn any triangle ABC, if the angle bisector of ∠A and perpendicular bisector of BC intersect, prove that they intersect on the circumcircle of the triangle ABC.
View SolutionIn the given triangle ABC, find AE.
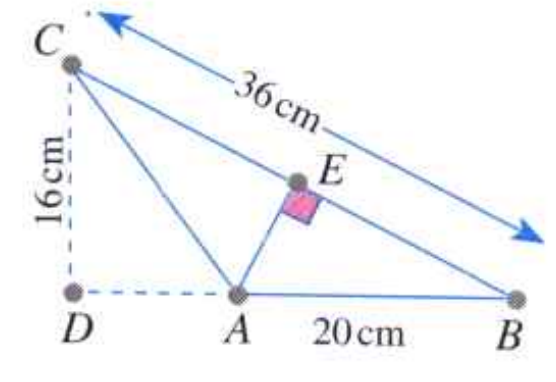
View SolutionWhich of the following holds goods for any triangle ABC ?
View SolutionIf in a triangle ABC,cosA=sinB2sinC then the triangle ABC , is
View SolutionIn a triangle ABC
View SolutionIf the perimeter of the triangle formed by feet of altitudes of the triangle ABC is equal to four times the circumradius of ΔABC, then identify the type of ΔABC
View SolutionIn a triangle ABC,r=
View SolutionIn the following figure G, is centroid of the triangles ABC.
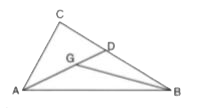
Prove that
Area (Δ AGB )=13× Area (ΔABC)
View SolutionThe triangle ABC, where A is (2, 6), B is (-3, 5) and C is (4, 7), is reflected in the y-axis to triangle A'B'C'. Triangle A'B'C' is then reflected in the origin to triangle A"B"C''.
Write down a single transformation that maps triangle ABC onto triangle A"B"C".
View Solution
