There is a point P inside an equilateral of side a whose distances from vertices A, B and C are 3, 4 and 5, respectively. Rotate the triangle and P through about C. Let A go to A' and P to P'. Then the area of (in sq. units) is
8
12
16
6
The correct Answer is:D
To solve the problem, we need to find the area of triangle ΔPAP′ after rotating point P and vertex A through 60∘ about point C.
1. Identify the Given Distances:
- The distances from point P to vertices A, B, and C are given as:
- AP=3
- BP=4
- CP=5
2. Understand the Rotation:
- When we rotate the triangle ABC and point P through 60∘ about point C, the following transformations occur:
- Vertex A moves to A′.
- Point P moves to P′.
3. Calculate Distances After Rotation:
- After rotation, the distances remain the same:
- AP′=AP=3
- BP′=BP=4
- CP′=CP=5
4. Determine the Angle:
- The angle ∠CPP′ is 60∘ due to the rotation.
- Since CP=CP′ and AP=AP′, we can analyze triangle CPP′.
5. Use the Law of Cosines:
- In triangle CPP′, we can find PP′ using the Law of Cosines:
PP′=√CP2+CP′2−2⋅CP⋅CP′⋅cos(60∘)
- Substituting the values:
PP′=√52+52−2⋅5⋅5⋅12=√25+25−25=√25=5
6. Calculate the Area of Triangle PAP′:
- The area of triangle PAP′ can be calculated using the formula:
Area=12×AP×AP′×sin(∠PAP′)
- Since ∠PAP′=90∘ (as derived from the properties of the triangle), we have:
Area=12×3×4×1=12×12=6
7. Final Answer:
- The area of triangle PAP′ is 6 square units.
- The distances from point P to vertices A, B, and C are given as:
- AP=3
- BP=4
- CP=5
- When we rotate the triangle ABC and point P through 60∘ about point C, the following transformations occur:
- Vertex A moves to A′.
- Point P moves to P′.
- After rotation, the distances remain the same:
- AP′=AP=3
- BP′=BP=4
- CP′=CP=5
- The angle ∠CPP′ is 60∘ due to the rotation.
- Since CP=CP′ and AP=AP′, we can analyze triangle CPP′.
- In triangle CPP′, we can find PP′ using the Law of Cosines:
PP′=√CP2+CP′2−2⋅CP⋅CP′⋅cos(60∘)
- Substituting the values:
PP′=√52+52−2⋅5⋅5⋅12=√25+25−25=√25=5
- The area of triangle PAP′ can be calculated using the formula:
Area=12×AP×AP′×sin(∠PAP′)
- Since ∠PAP′=90∘ (as derived from the properties of the triangle), we have:
Area=12×3×4×1=12×12=6
- The area of triangle PAP′ is 6 square units.
Topper's Solved these Questions
- BOOK - CENGAGE ENGLISHCHAPTER - PROPERTIES AND SOLUTIONS OF TRIANGLEEXERCISE - Multiple correct answer type24videos
PROPERTIES AND SOLUTIONS OF TRIANGLE
- BOOK - CENGAGE ENGLISHCHAPTER - PROPERTIES AND SOLUTIONS OF TRIANGLEEXERCISE - Linked comprehension type34videos
PROPERTIES AND SOLUTIONS OF TRIANGLE
- BOOK - CENGAGE ENGLISHCHAPTER - PROPERTIES AND SOLUTIONS OF TRIANGLEEXERCISE - Concept application exercise 5.114videos
PROPERTIES AND SOLUTIONS OF TRIANGLE
- BOOK - CENGAGE ENGLISHCHAPTER - PROGRESSION AND SERIESEXERCISE - ARCHIVES (MATRIX MATCH TYPE )1videos
PROGRESSION AND SERIES
- BOOK - CENGAGE ENGLISHCHAPTER - RELATIONS AND FUNCTIONSEXERCISE - Archives(Matrix Match Type)1videos
RELATIONS AND FUNCTIONS
Similar Questions
Let a point P lies inside an equilateral △ABC such that its perpendicular distances from sides are P1,P2,P3.If side length of △ABC is 2 unit then
View SolutionIf the coordinates of two points A and B are (3, 4) and (5,−2) , respectively, find the coordinates of any point P if PA=PB. Area of PAB is 10 sq. units.
View SolutionIf the coordinates of two points A and B are (3, 4) and (5,−2) , respectively, find the coordinates of any point P if PA=PB. Area of PAB is 10 sq. units.
View SolutionIf the coordinates of two points A and B are (3, 4) and (5,−2) , respectively, find the coordinates of any point P if PA=PB. Area of PAB is 10 sq. units.
View SolutionIf P1,P2 and P3 are the altitudes of a triangle from vertices A,B and C respectively and Δ is the area of the triangle, then the value of 1P1+1P2−1P3=
View SolutionABC is a right triangle, right - angled at the vertex A. A circle is drawn to touch the sides AB and AC at points P and Q respectively such that the other end points of the diameters passing through P and Q lie on the side BC. IF AB = 6 units, then the area (in sq. units) of the circular sector which lies inside the triangle is
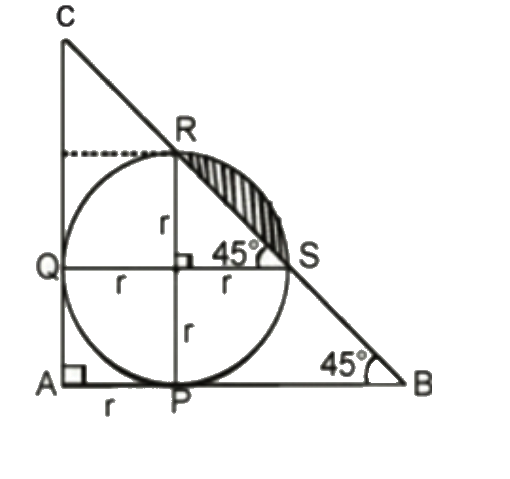 View Solution
View SolutionThe point P(α,α+1) will lie inside the triangle whose vertices are A(0,3),B(−2,0) and C(6,1) if
View SolutionIf in a ΔABC, the altitudes from the vertices A, B, C on opposite sides are in H.P, then sin A, sin B, sin C are in
View SolutionIf in ΔABC, sides a, b, c are in A.P. then
View SolutionLet a,b,c be the sides of triangle whose perimeter is P and area is A, then
View Solution

