Let a point P lies inside an equilateral △ABC such that its perpendicular distances from sides are P1,P2,P3.If side length of △ABC is 2 unit then
(P1+P2+P3) is equal to √3
(P1+P2+P3) is equal to 4√3
Area of △=√3 Sq unit
Area of △ABC=3 Sq unit
The correct Answer is:A, C
To solve the problem, we need to find the sum of the perpendicular distances from point P inside an equilateral triangle ABC to its sides, given that the side length of the triangle is 2 units.
1. Understand the Geometry:
- We have an equilateral triangle ABC with side length a=2 units.
- Let P be a point inside the triangle, and let P1,P2,P3 be the perpendicular distances from point P to sides BC,CA, and AB respectively.
2. Calculate the Area of Triangle ABC:
- The area A of an equilateral triangle can be calculated using the formula:
A=√34a2
- Substituting a=2:
A=√34×22=√34×4=√3
3. Express the Area in Terms of Distances:
- The area of triangle ABC can also be expressed as the sum of the areas of the three smaller triangles formed by point P:
A=Area(APB)+Area(BPC)+Area(CPA)
- The area of each triangle can be calculated using the formula:
Area=12×base×height
- For triangle APB:
Area(APB)=12×AB×P1=12×2×P1=P1
- For triangle BPC:
Area(BPC)=12×BC×P2=12×2×P2=P2
- For triangle CPA:
Area(CPA)=12×CA×P3=12×2×P3=P3
4. Combine the Areas:
- Thus, we can write:
A=P1+P2+P3
- Since we already found A=√3, we have:
P1+P2+P3=√3
5. Conclusion:
- The sum of the perpendicular distances from point P to the sides of triangle ABC is:
P1+P2+P3=√3
Final Answers:
- The area of triangle ABC is √3.
- The sum of the perpendicular distances P1+P2+P3 is √3.
- We have an equilateral triangle ABC with side length a=2 units.
- Let P be a point inside the triangle, and let P1,P2,P3 be the perpendicular distances from point P to sides BC,CA, and AB respectively.
- The area A of an equilateral triangle can be calculated using the formula:
A=√34a2
- Substituting a=2:
A=√34×22=√34×4=√3
- The area of triangle ABC can also be expressed as the sum of the areas of the three smaller triangles formed by point P:
A=Area(APB)+Area(BPC)+Area(CPA)
- The area of each triangle can be calculated using the formula:
Area=12×base×height
- For triangle APB:
Area(APB)=12×AB×P1=12×2×P1=P1
- For triangle BPC:
Area(BPC)=12×BC×P2=12×2×P2=P2
- For triangle CPA:
Area(CPA)=12×CA×P3=12×2×P3=P3
- Thus, we can write:
A=P1+P2+P3
- Since we already found A=√3, we have:
P1+P2+P3=√3
- The sum of the perpendicular distances from point P to the sides of triangle ABC is:
P1+P2+P3=√3
- The area of triangle ABC is √3.
- The sum of the perpendicular distances P1+P2+P3 is √3.
Topper's Solved these Questions
- TEST PAPERBOOK - ALLENCHAPTER - TEST PAPEREXERCISE - MATHEMATICS
25 Videos
- TEST PAPERBOOK - ALLENCHAPTER - TEST PAPEREXERCISE - PHYSICS SECTION-I
2 Videos
- TEST PAPERBOOK - ALLENCHAPTER - TEST PAPEREXERCISE - Chemistry
54 Videos
- SEQUENCE AND PROGRESSIONBOOK - ALLENCHAPTER - SEQUENCE AND PROGRESSIONEXERCISE - Exercise (JA)
12 Videos
- TEST PAPERSBOOK - ALLENCHAPTER - TEST PAPERSEXERCISE - PHYSICS
4 Videos
Similar Questions
In an equilateral triangle ABC, BE is perpendicular to side CA. Prove that:
AB2+BC2+CA2=4BE2
View SolutionThe P lies on side AB of an equilateral triangle ABC. Arrange AC, AP and CP in descending order.
View SolutionLet the point P lies in the interior of an equilateral triangle with side lengths 2 units, each. Find the sum of the shortest distances from P to the sides of the triangle.
View SolutionIn equilateral triangle ABC with interior point D, if the perpendicular distances from D to the sides of 4,5, and 6, respectively, are given, then find the area of ABC.
View SolutionThrough the centroid of an equilateral triangle, a line parallel to the base is drawn. On this line, an arbitrary point P is taken inside the triangle. Let h denote the perpendicular distance of P from the base of the triangle. Let h1andh2 be the perpendicular distance of P from the other two sides of the triangle . Then :
View SolutionP is any point inside the triangle ABC. Prove that : ∠BPC>∠BAC.
View SolutionIf r1,r2,r3 in triangle be in H.P., then the sides are :
View SolutionThere is a point P inside an equilateral ΔABC of side a whose distances from vertices A, B and C are 3, 4 and 5, respectively. Rotate the triangle and P through 60∘ about C. Let A go to A' and P to P'. Then the area of ΔPAP' (in sq. units) is
View SolutionTriangle ABC is isosceles with AB=ACandBC=65cm. P is a point on BC such that the perpendiculardistances from P to ABandAC are 24cmand36cm, respectively. The area of triangle ABC (in sq cm is)
View SolutionSides AB and AC in an equilateral triangle ABC with side length 3 is extended to form two rays from point A as shown in the figure. Point P is chosen outside the triangle ABC and between the two rays such that ∠ABP+∠BCP=180∘. If the maximum length of CP is M, then M2/2 is equal to :
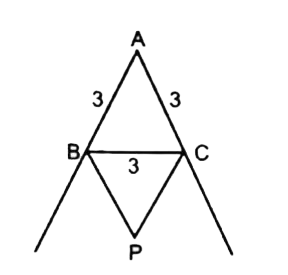
View Solution