The area enclosed by $y = x^{2} + cos x and its normal at x = \frac{π}{2}$ in the first quadrant is

A

$\frac{π^{5}}{32} - \frac{π^{4}}{64} + \frac{π^{3}}{32} + 1$

B

$\frac{π^{5}}{16} - \frac{π^{4}}{32} + \frac{π^{3}}{24} - 1$

C

$\frac{π^{5}}{32} - \frac{π^{4}}{32} + \frac{π^{3}}{16}$

D

$\frac{π^{5}}{32} - \frac{π^{4}}{32} + \frac{π^{3}}{24} + 1$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:D

$f (x) = x^{2} + cos x$
$\Rightarrow f' (x) = 2 x - sin x$
$\Rightarrow f' (\frac{π}{4}) = π - 1$
$\Rightarrow Equation of normal at x = \frac{π}{2}$ is
$(y - \frac{π^{4}}{4}) = \frac{1}{1 - π} (x - \frac{π}{2})$
$It meets x-axis at x = \frac{(π - 1) π^{2}}{4} + \frac{π}{2}$
Also $f' (x) = 2 x - sin x > 0 for x > 0 and < 0 for x < 0$
So f(x) increases for $x \in (0, \infty) and decreases for x \in (- \infty, 0)$
Graph of the function is as shown in the followin figure.

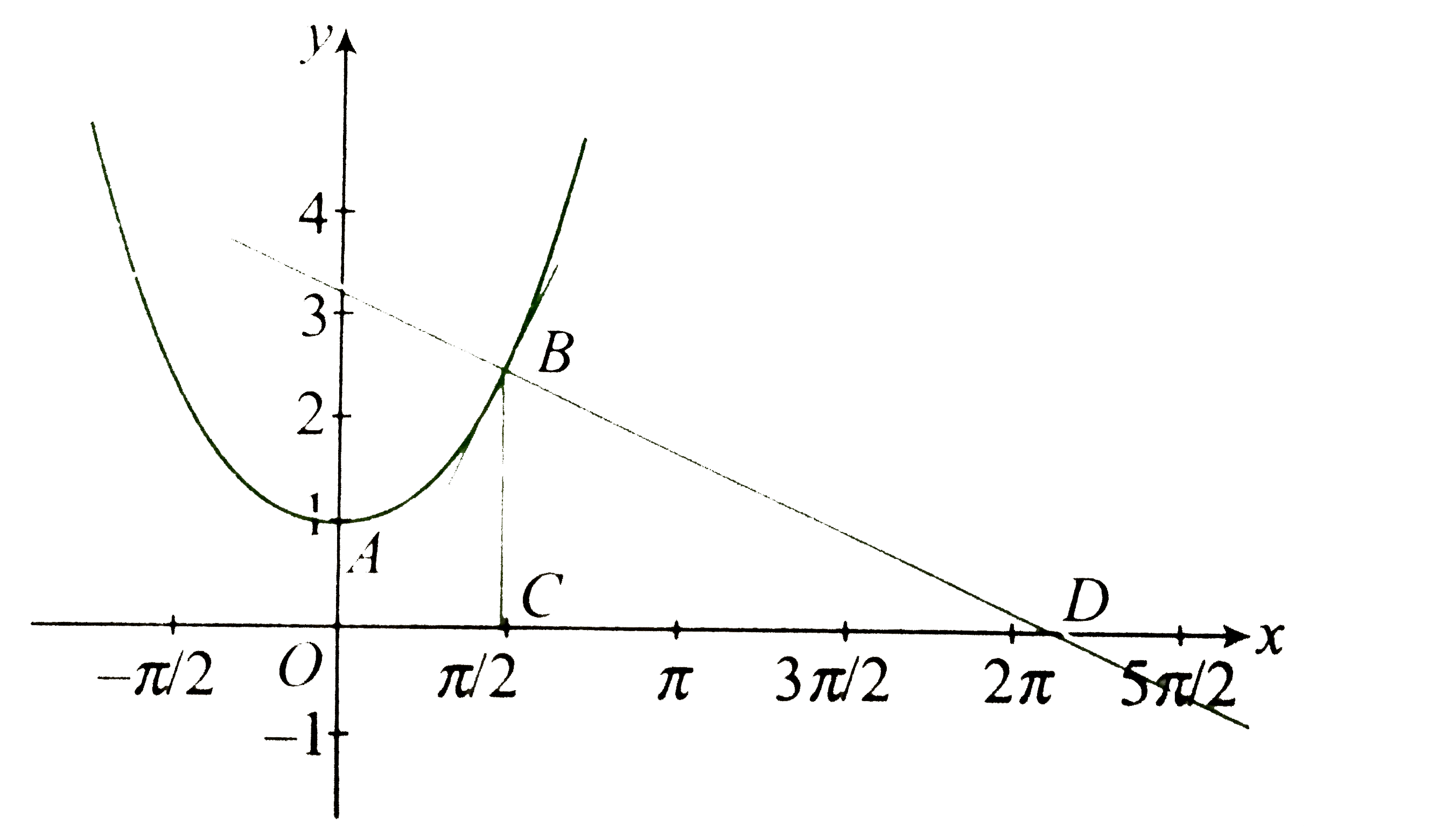
Required area
=Area OABCO+Area of $Δ B C D$
$= π / 2 \int 0 (x^{2} + cos x) d x + \frac{1}{2} [\frac{(π - 1) π^{2}}{4} + \frac{π}{2} - \frac{π}{2}] \times \frac{π^{2}}{4}$
$= {[\frac{x^{3}}{3} + sin x]}_{0}^{π / 2} + \frac{(π - 1) π^{2}}{8}$
$= \frac{π^{3}}{24} + 1 + \frac{π^{4}}{32} (π - 1)$
$= \frac{π^{5}}{32} - \frac{π^{4}}{32} + \frac{π^{3}}{24} + 1$

Updated on:21/07/2023

|

Class 12 MATHS APPLICATION OF INTEGRALS

Topper's Solved these Questions

Similar Questions

CENGAGE ENGLISH-AREA-Exercises - Single Correct Answer Type

Home
Ask Doubt
Profile