The area enclosed between the curve $y^{2} (2 a - x) = x^{3}$ and the line x=2 above the x-axis is

A

$π a^{2}$ sq. units

B

$\frac{3 π a^{2}}{2}$ sq. units

C

$2 π a^{2}$ sq. units

D

$3 π a^{2}$ sq. units

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

The required area $A = \int_{0}^{2 a} \sqrt{\frac{x^{3}}{2 a - x}} d x$

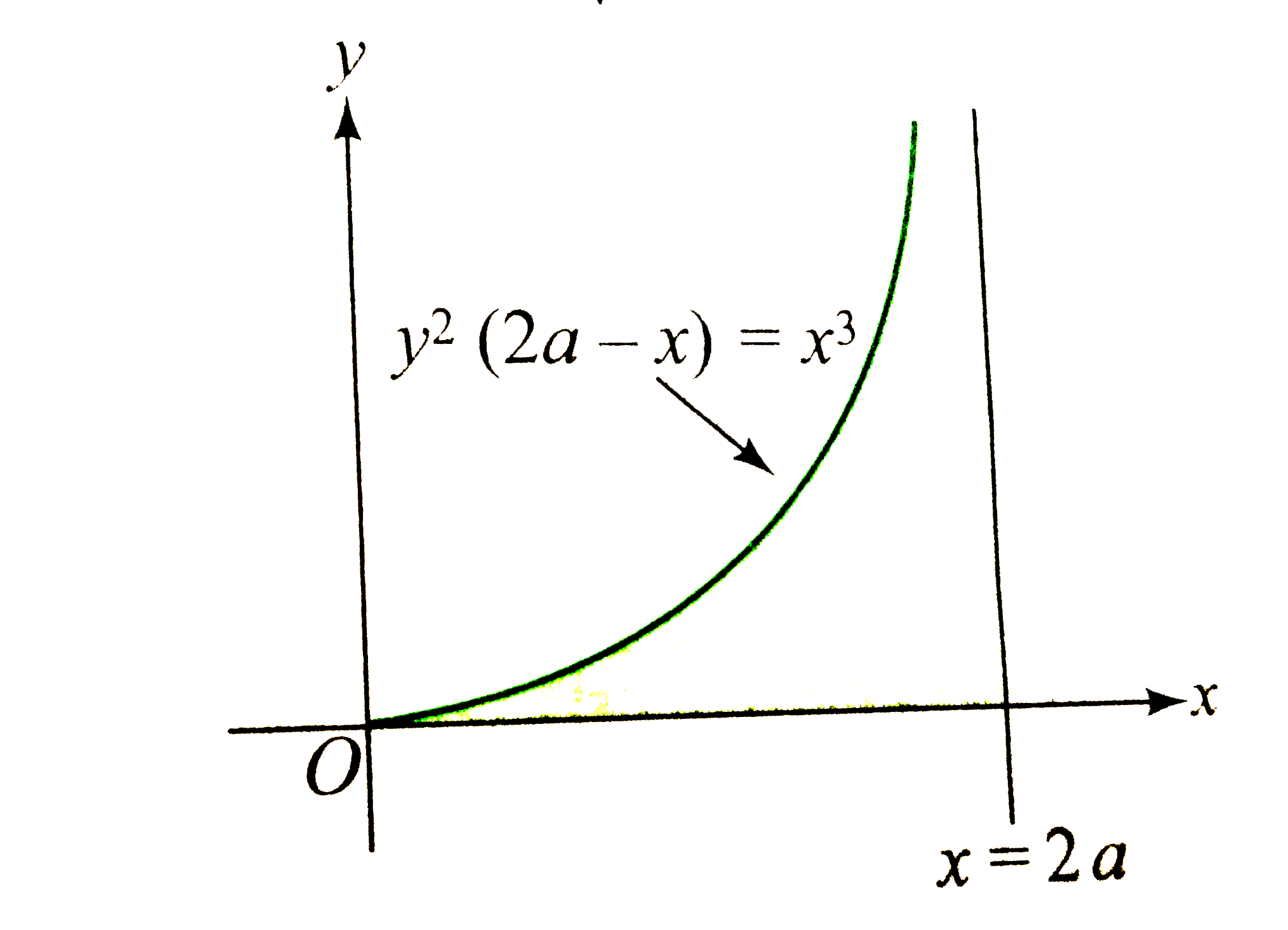
$Put x = 2 a {sin}^{2} θ$
$\Rightarrow d x = 2 a sin θ cos θ d θ$
$\Rightarrow A = 8 a^{2} \int_{0}^{π} {(\frac{1 - cos 2 θ}{2})}^{2} d θ$
$= 2 a^{2} \int_{0}^{π} (1 - 2 cos 2 θ + {cos}^{2} 2 θ) d θ$
$2 a^{2} \int_{0}^{π} (1 - 2 cos 2 θ + \frac{1 + cos 4 θ}{2}) d θ = \frac{3 π a^{2}}{2}$

Updated on:21/07/2023

|

Class 12 MATHS APPLICATION OF INTEGRALS

Topper's Solved these Questions

Similar Questions

CENGAGE ENGLISH-AREA-Exercises - Single Correct Answer Type

Home
Ask Doubt
Profile