Find the equations of the circles which pass through the origin and cut off chords of length $a$ from each of the lines $y = x and y = - x$

Video Solution

Text Solution

Verified by Experts

The correct Answer is: $x^{2} + y^{2} \pm \sqrt{2} a x = 0$ and $x^{2} + y^{2} \pm \sqrt{2} a y = 0$

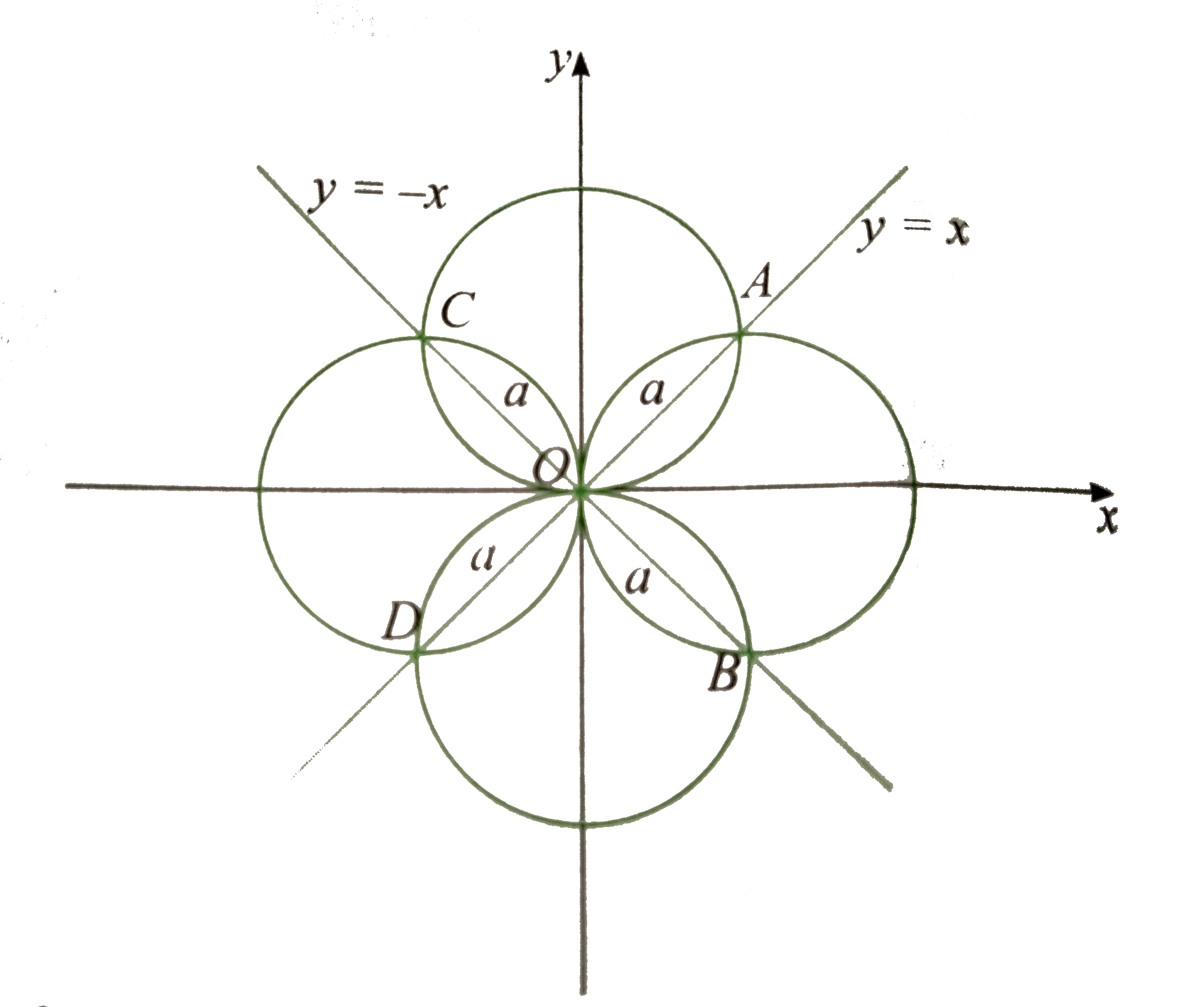
In the figure, length of chords OA and AB that cut off by the circles is a.
$∴ A \equiv (\frac{a}{\sqrt{2}}, \frac{a}{\sqrt{2}})$ and $B \equiv (\frac{a}{\sqrt{2}}, - \frac{a}{\sqrt{2}})$ , which are end points of diameters.
Therefore, the equation of circle is
$(x - \frac{a}{\sqrt{2}}) (x - \frac{a}{\sqrt{2}}) + (y - \frac{a}{\sqrt{2}}) (y + \frac{a}{\sqrt{2}}) = 0$
or $x^{2} + y^{2} - \sqrt{2} a x = 0$
Circles with AC and BD as diametere are given by $x^{2} + y^{2} \pm \sqrt{2} a y = 0$

|

Updated on:21/07/2023

Class 12 MATHS CIRCLE

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
Find the equation of the circle which passes through the origin and cuts off intercepts -2 and 3 from the coordinate axes .
Ax^(2) + y^(2) + 2x + 3y = 0
B $x^{2} + y^{2} + 2 x - 3 y = 0$
C $x^{2} + y^{2} - 2 x + 3 y = 0$
D $x^{2} + y^{2} - 2 x - 3 y = 0$

CENGAGE ENGLISH-CIRCLE -CONCEPT APPLICATION EXERCISE 4.3

Home
Ask Doubt
Profile