Find the angle between the two tangents from the origin to the circle (x−7)2+(y+1)2=25
The correct Answer is:90∘
Centre of the circle is C(7,-1) and radius , CM=5.
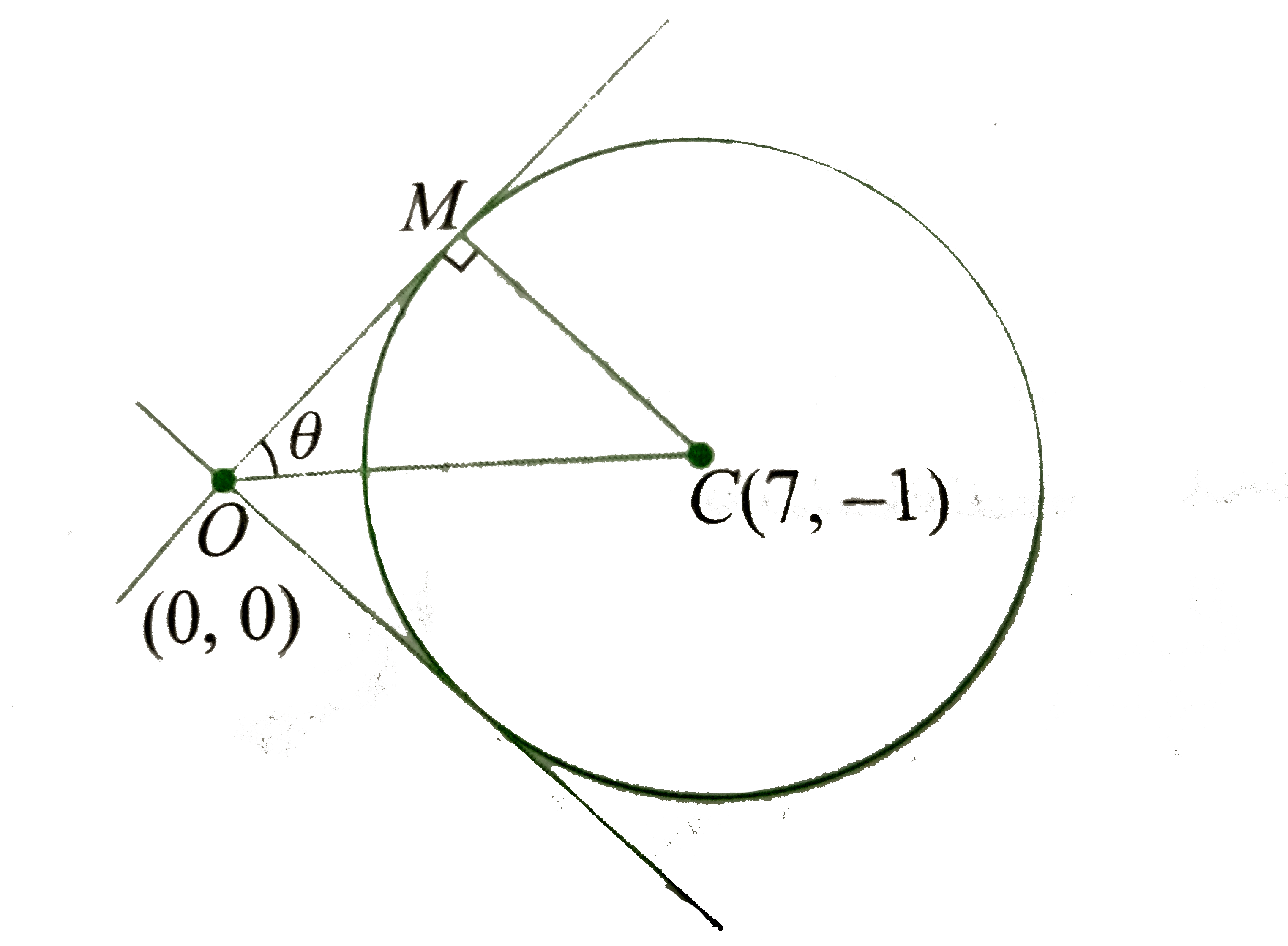
OC=√72+(−1)2=5√2
∴sinθ=CMOC=55√2=1√2
⇒θ=45∘
Hence, angle between tangents is 90∘.
Topper's Solved these Questions
- CIRCLE Book:CENGAGE ENGLISHChapter:CIRCLE Exercise:CONCEPT APPLICATION EXERCISE 4.4
Explore 4 Videos
- CIRCLE Book:CENGAGE ENGLISHChapter:CIRCLE Exercise:CONCEPT APPLICATION EXERCISE 4.5
Explore 5 Videos
- CIRCLE Book:CENGAGE ENGLISHChapter:CIRCLE Exercise:CONCEPT APPLICATION EXERCISE 4.2
Explore 2 Videos
- BINOMIAL THEOREMBook:CENGAGE ENGLISHChapter:BINOMIAL THEOREMExercise:Matrix
Explore 4 Videos
- CIRCLESBook:CENGAGE ENGLISHChapter:CIRCLESExercise:Comprehension Type
Explore 8 Videos
Similar Questions
Find the angle between the tangents drawn from the origin to the parabolas y2=4a(x−a)
View SolutionFind the angle between the tangents drawn from the origin to the parabolas y2=4a(x−a) (a) 90∘ (b) 30∘ (c) tan−1(12) (d) 45∘
View SolutionFind the angle between the pair of tangents from the point (1,2) to the ellipse 3x2+2y2=5.
View SolutionThe angle between the tangents drawn from the origin to the circle x2+y2+4x−6y+4=0 is
View SolutionFind the angle between the pair of
tangents drawn from (1,3) to the circle
x2+y2−2x+4y−11=0
View SolutionThe angle between the pair of tangents from the point (1,12) to the circle x2+y2+4x+2y−4=0 is
View SolutionFind the angle between the pair of
tangents drawn from (0,0) to the circle
x2+y2−14x+2y+25=0.
View SolutionFind the angle between two tangents drawn from the point ( 1,4) to the parabola y2=12x
View SolutionFind the equation of the two tangents from the point (0,1) to the circle x2+y2−2x+4y=0
View SolutionFind the angle between the tangents
drawn from (3,2) to the circle
x2+y2−6x+4y−2=0
View Solution
