A variable chord of the circle x2+y2=4 is drawn from the point P(3,5) meeting the circle at the point A and B. A point Q is taken on the chord such that 2PQ=PA+PB . The locus of Q is x2+y2+3x+4y=0 x2+y2=36 x2+y2=16 x2+y2−3x−5y=0
x2+y2+3x+4y=0
x2+y2=36
x2+y2=16
x2+y2−3x−5y=0
The correct Answer is:4
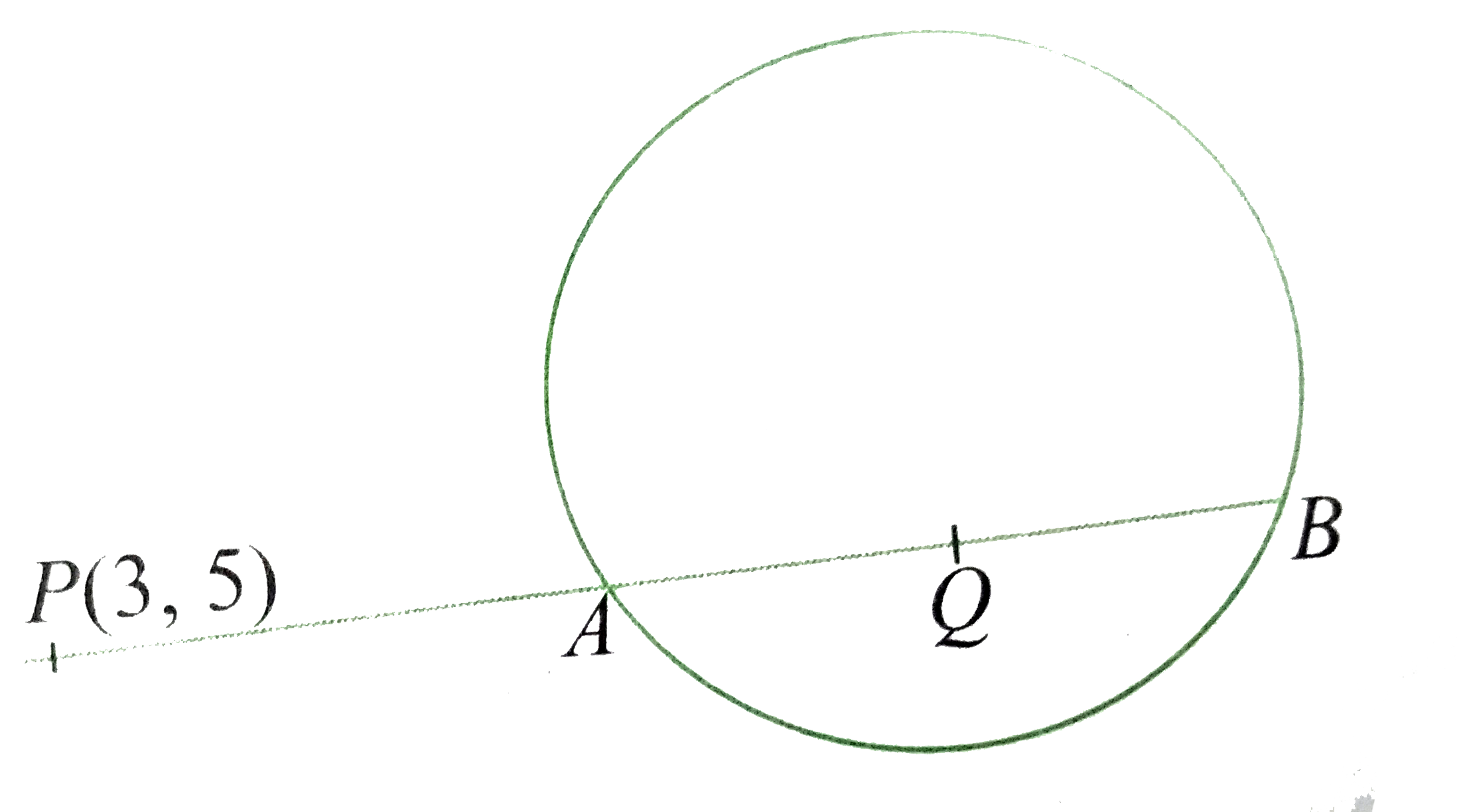
2PQ=PA+PB
or PQ−PA=PB−PQ
or AQ=QB
Therefore, Q is the midpoint of AB.
Let Q has coordinates (h,k).
Then the equation of chord AB is given by T=S1
or hx+ky−4=h2+k2−4
This variable chord passes through the point P(3,5). Therefore,
3h+5k=h2+k2
or x2+y2−3x−5y=0
which is the required locus.
Topper's Solved these Questions
- CIRCLE Book:CENGAGE ENGLISHChapter:CIRCLE Exercise:Multiple Correct Anser Type
Explore 29 Videos
- CIRCLE Book:CENGAGE ENGLISHChapter:CIRCLE Exercise:Linked Comprehension Type (For Problem 1-3)
Explore 3 Videos
- CIRCLE Book:CENGAGE ENGLISHChapter:CIRCLE Exercise:CONCEPT APPLICATION EXERCISE 4.20
Explore 1 Video
- BINOMIAL THEOREMBook:CENGAGE ENGLISHChapter:BINOMIAL THEOREMExercise:Matrix
Explore 4 Videos
- CIRCLESBook:CENGAGE ENGLISHChapter:CIRCLESExercise:Comprehension Type
Explore 8 Videos
Similar Questions
A variable chord of circle x2+y2+2gx+2fy+c=0 passes through the point P(x1,y1). Find the locus of the midpoint of the chord.
View SolutionFrom the point A(0,3) on the circle x2+4x+(y−3)2=0, a chord AB is drawn and extended to a point P, such that AP=2AB. The locus of P is
View SolutionFind the equation of tangents to circle x2+y2−2x+4y−4=0
drawn from point P(2,3).
View SolutionIf the tangents are drawn to the circle x2+y2=12 at the point where it meets the circle x2+y2−5x+3y−2=0, then find the point of intersection of these tangents.
View SolutionTangents are drawn to the circle x2+y2=9 at the points where it is met by the circle x2+y2+3x+4y+2=0 . Find the point of intersection of these tangents.
View SolutionFrom the point A (0, 3) on the circle x2+4x+(y−3)2=0 a chord AB is drawn & extended to a M point such that AM=2AB. The equation of the locus of M is: (A)x2+8x+y2=0 (B)x2+8x+(y−3)2=0 (C)(x−3)2+8x+y2=0 (D)x2+8x+8y=0
View SolutionA tangent to the circle x2+y2=1 through the point (0, 5) cuts the circle x2+y2=4 at P and Q. If the tangents to the circle x2+y2=4 at P and Q meet at R, then the coordinates of R are
View SolutionThe length of the chord of contact of the tangents drawn from the point (−2,3) to the circle x2+y2−4x−6y+12=0 is:
View SolutionA tangent is drawn to the circle 2(x2+y2)−3x+4y=0 and it touches the circle at point A. If the tangent passes through the point P(2, 1),then PA=
View SolutionIf two distnct chords of the circle x2+y2−2x−4y=0 drawn from the point P (a,b) are bisected by y-axis then a) (b+2)2>4a b) (b−2)2>4a c)(b−2)2>2a d) (b+2)2>a
View Solution