The range of values of λ,(λ>0) such that the angle θ between the pair of tangents drawn from (λ,0) to the circle x2+y2=4 lies in (π2,2π3) is (a) (4√3,2√2) (b) (0,√2) (c) (1,2) (d) none of these
(4/√3,2√2)
(0,√2)
(1,2)
none of these
The correct Answer is:1
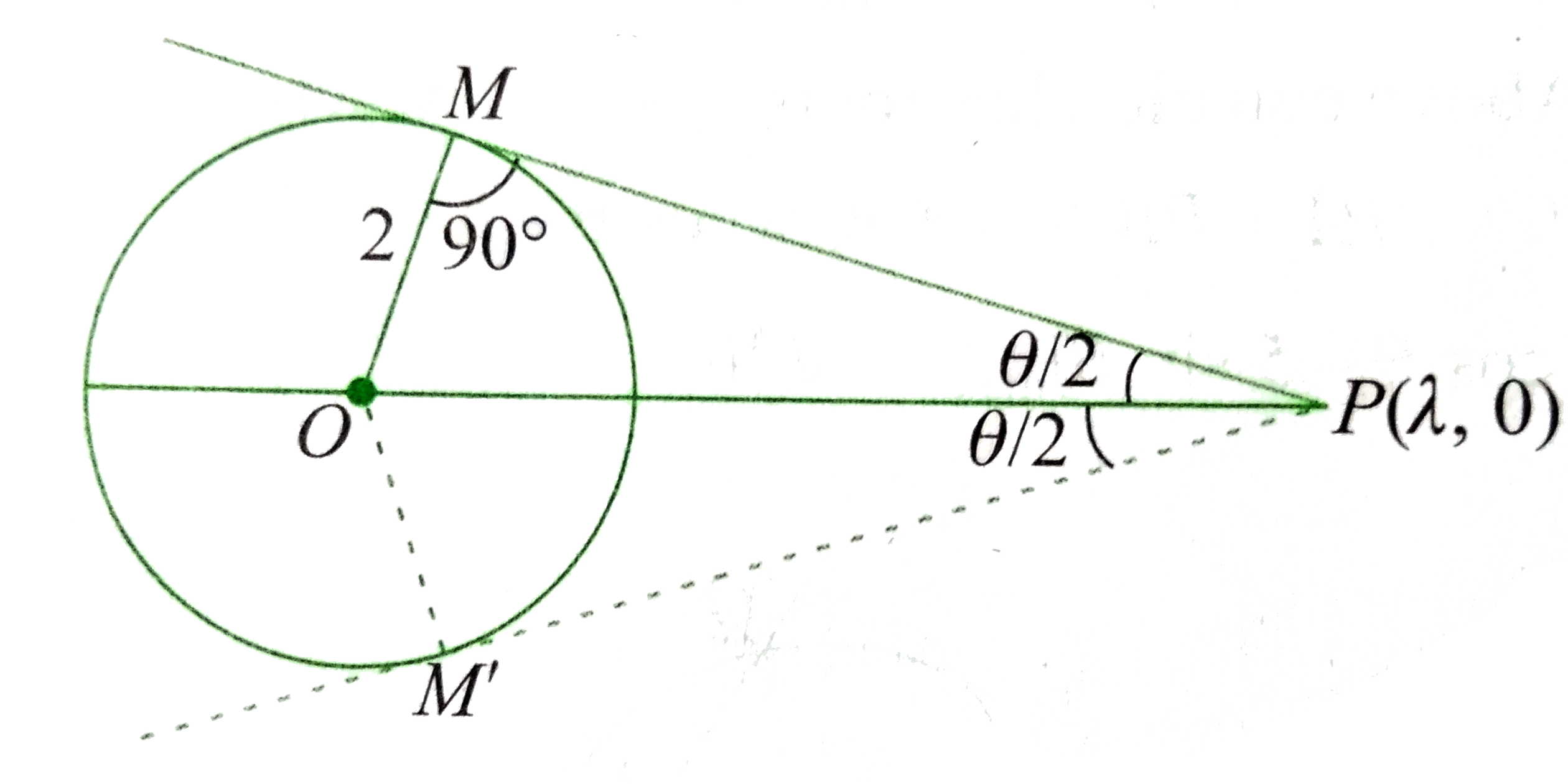
We have π2<θ<2π3,i.e., π4<θ2<π3
or 1√2<sin.θ2<√32
But sin.θ2=2λ or 1√2<2λ<√32
or 4√3<λ<2√2
Topper's Solved these Questions
- BOOK - CENGAGE ENGLISHCHAPTER - CIRCLE EXERCISE - Multiple Correct Anser Type29videos
CIRCLE
- BOOK - CENGAGE ENGLISHCHAPTER - CIRCLE EXERCISE - Linked Comprehension Type (For Problem 1-3)3videos
CIRCLE
- BOOK - CENGAGE ENGLISHCHAPTER - CIRCLE EXERCISE - CONCEPT APPLICATION EXERCISE 4.201videos
CIRCLE
- BOOK - CENGAGE ENGLISHCHAPTER - BINOMIAL THEOREMEXERCISE - Matrix4videos
BINOMIAL THEOREM
- BOOK - CENGAGE ENGLISHCHAPTER - CIRCLESEXERCISE - Comprehension Type8videos
CIRCLES
Similar Questions
The range of values of a such that the angle θ between the pair of tangents drawn from (a,0) to the circle x2+y2=1 satisfies π2<θ<π is
View SolutionThe exhaustive range of value of a such that the angle between the pair of tangents drawn from (a,a) to the circle x2+y2−2x−2y−6=0 lies in the range (π3,π) is
View SolutionFind the angle between the pair of
tangents drawn from (1,3) to the circle
x2+y2−2x+4y−11=0View SolutionThe value of (lim)x→2√1+√2+x−√3x−2is (a) 18√3 (b) 14√3 (c) 0 (d) none of these
View SolutionIf tangents PQ and PR are drawn from a point on the circle x2+y2=25 to the ellipse x216+y2b2=1,(b<4), so that the fourth vertex S of parallelogram PQSR lies on the circumcircle of triangle PQR , then the eccentricity of the ellipse is
(a)√54
(b) √74
(c) √72
(d) √53View SolutionAn infinite number of tangents can be drawn from (1,2) to the circle x2+y2−2x−4y+λ=0 . Then find the value of λ.
View Solution√3∫π0dx1+2sin2x= (A) −π (B) 0 (C) π (D) none of these
View SolutionThe value of the definite integral ∫π20√tanxdx is √2π (b) π√2 2√2π (d) π2√2
View SolutionThe area of the circle x2+y2=16exterior to the parabola y2=6xis(A) 43(4π−√3) (B) 43(4π+√3)(C) 43(8π−√3) (D) 43(8π+√3)
View SolutionIf the tangents from the point (λ,3) to the ellipse x29+y24=1 are at right angles then λ is
View Solution

