The angle between the pair of tangents drawn from a point $P$ to the circle $x^{2} + y^{2} + 4 x - 6 y + 9 {sin}^{2} α + 13 {cos}^{2} α = 0$ is $2 α$ . then the equation of the locus of the point $P$ is a. $x^{2} + y^{2} + 4 x - 6 y + 4 = 0$ b. $x^{2} + y^{2} + 4 x - 6 y - 9 = 0$ c. $x^{2} + y^{2} + 4 x - 6 y - 4 = 0$ d, $x^{2} + y^{2} + 4 x - 6 y + 9 = 0$

A

$x^{2} + y^{2} + 4 x - 6 y + 4 = 0$

B

$x^{2} + y^{2} + 4 x - 6 y - 9 = 0$

C

$x^{2} + y^{2} + 4 x - 6 y - 4 = 0$

D

$x^{2} + y^{2} + 4 x - 6 y + 9 = 0$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:4

The center of the circle
$x^{2} + y^{2} + 4 x - 6 y + 9 {sin}^{2} α + 13 {cos}^{2} α = 0$
is $C (- 2, 3)$ and its radius is
$\sqrt{4 + 9 - 9 {sin}^{2} α - 13 {cos}^{2} α} = | 2 sin α |$

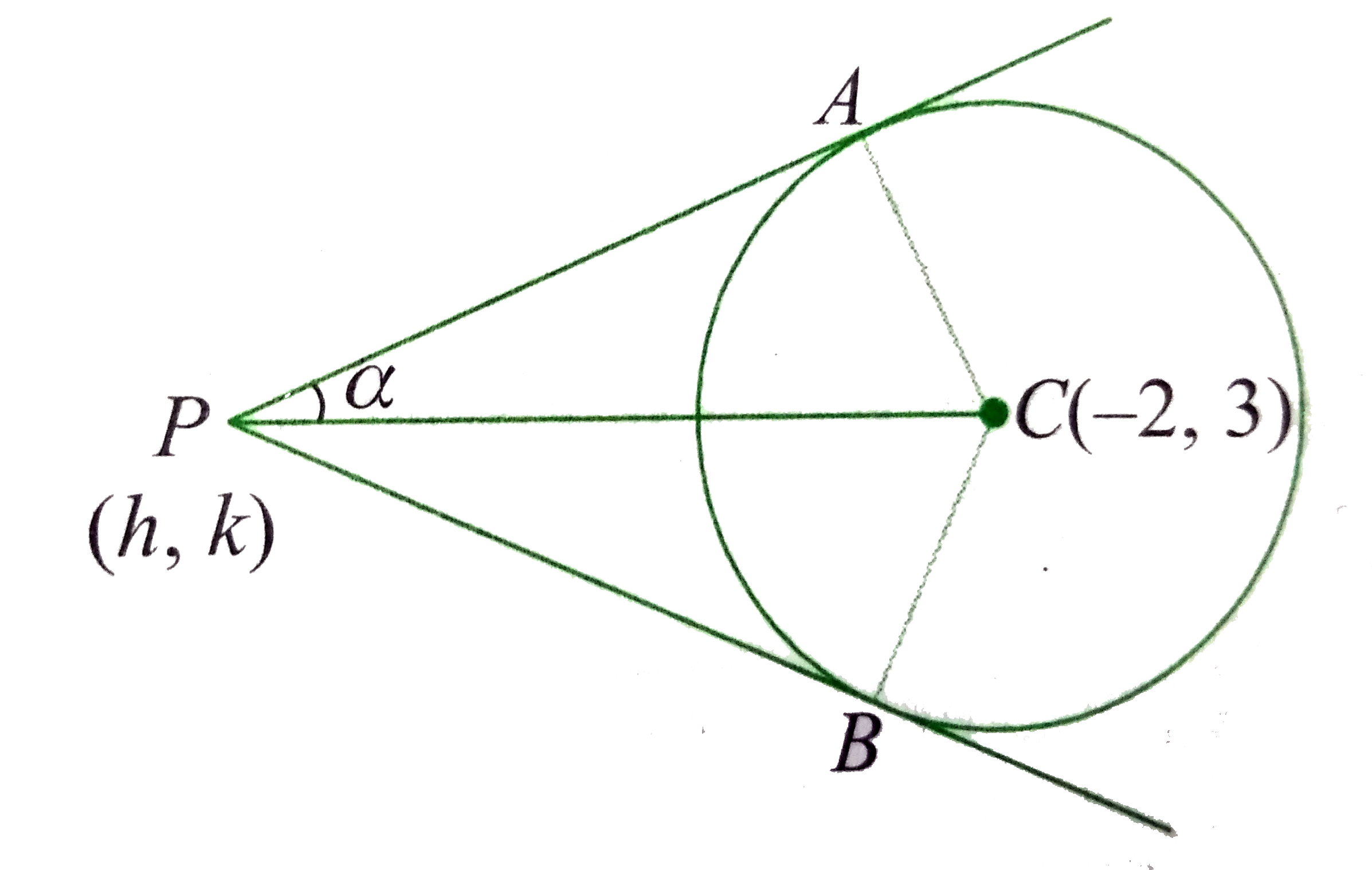
Let $P (h, k)$ be any point on the locus . Then $∠ A P C = α$
From the diagram,
$sin α = \frac{A C}{P C} = \frac{2 sin α}{\sqrt{{(h + 2)}^{2} + {(k - 3)}^{2}}}$
or ${(h + 2)}^{2} + {(k - 3)}^{2} = 4$
or $h^{2} + k^{2} + 4 h - 6 k + 9 = 0$
Thus, the required equation of the locus is
$x^{2} + y^{2} + 4 x - 6 y + 9 = 0$

|

Updated on:21/07/2023

Class 12 MATHS CIRCLE

Topper's Solved these Questions

Similar Questions

CENGAGE ENGLISH-CIRCLE -Excercises (Single Correct Answer Type)

Home
Ask Doubt
Profile