ABC is any triagnel inscribed in the circle x2+y2=r2 such that A is fixed point . If the external and internal bisectors of ∠A intersect the circle at D and E, respectively, then which of the following statements is true ΔADE ?
Its centroid is a fixed point.
Its circumcentre is a fixed point.
Its orthocentre is a fixed point.
none of these
The correct Answer is:1,2,3
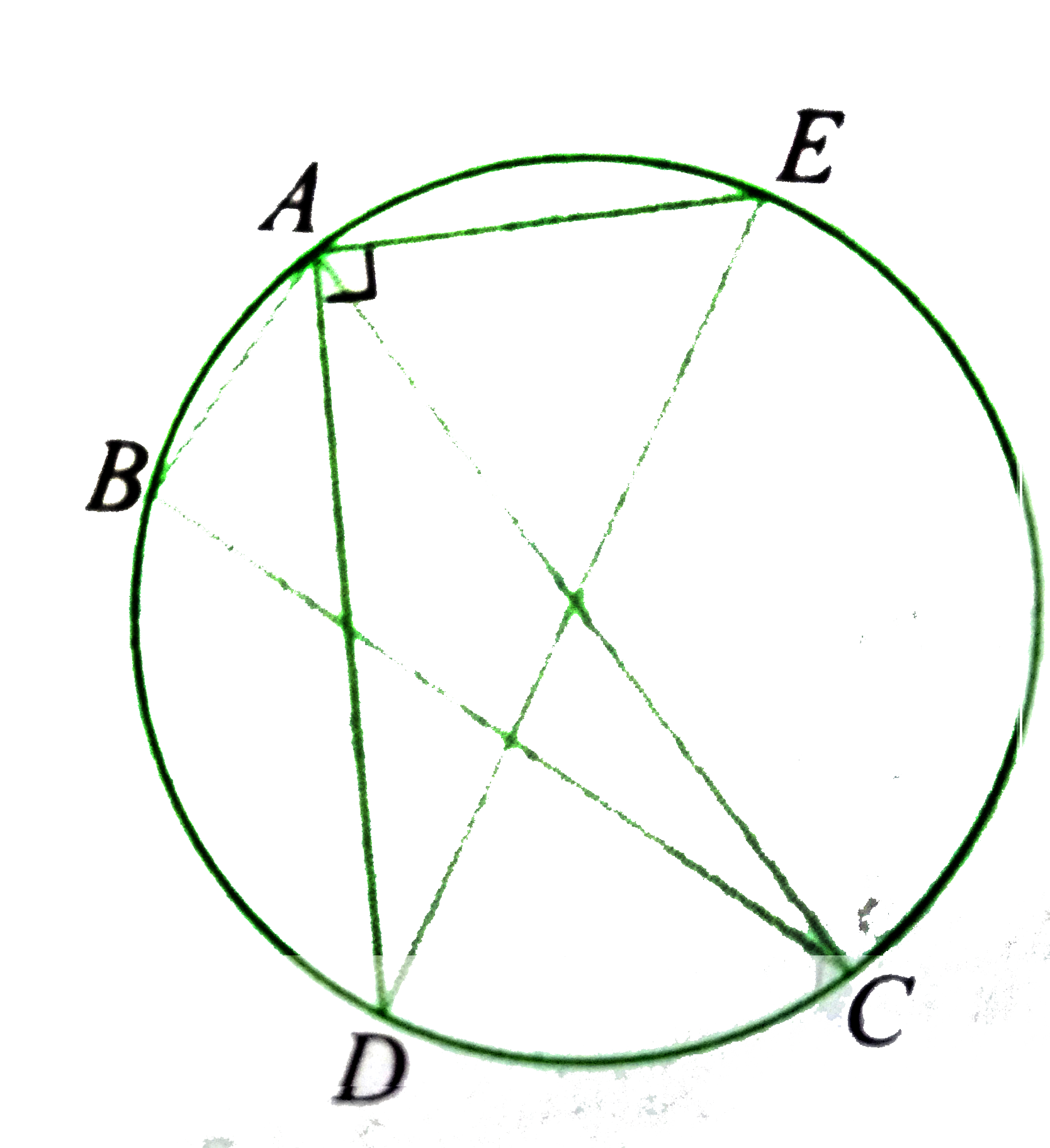
Orothocentre of ΔADE is A itself circumcentre is at origin. Hence, centroid is also a fixed point.
Topper's Solved these Questions
- BOOK - CENGAGE ENGLISHCHAPTER - CIRCLE EXERCISE - Linked Comprehension Type (For Problem 1-3)3videos
CIRCLE
- BOOK - CENGAGE ENGLISHCHAPTER - CIRCLE EXERCISE - For Problems43videos
CIRCLE
- BOOK - CENGAGE ENGLISHCHAPTER - CIRCLE EXERCISE - Excercises (Single Correct Answer Type)109videos
CIRCLE
- BOOK - CENGAGE ENGLISHCHAPTER - BINOMIAL THEOREMEXERCISE - Matrix4videos
BINOMIAL THEOREM
- BOOK - CENGAGE ENGLISHCHAPTER - CIRCLESEXERCISE - Comprehension Type8videos
CIRCLES
Similar Questions
If an equilateral triangle is inscribed in the circle x2+y2−6x−4y+5=0 then its side is
View SolutionThe line y=mx+c intersects the circle x2+y2=r2 in two distinct points if
View SolutionThe area of an equilateral triangle inscribed in the circle x2+y2+2gx+2fy+c=0 is
View SolutionA right angled isosceles triangle is inscribed in the circle x2+y2−4x−2y−4=0 then length of the side of the triangle is
View SolutionIf an equilateral triangle is inscribed in the circle x2+y2=a2, the length of its each side is
View SolutionArea of the equilateral △ inscribed in the circle x2+y2−7x+9y+5=0, is …………
View SolutionABC is a triangle. The bisector of the exterior angle at B and the bisector of ∠C intersect each other at D. Prove that ∠D=12∠A.
View SolutionA right angled isosceles triangle is inscribed in the circle x2+y2_4x−2y−4=0 then length of its side is
View SolutionA right angled isoceles triangle is inscribed in the circle x2+y2−6x+10y−38=0 then its area is (square units)
View SolutionThe locus of midpoints of the chord of the circle x2+y2=25 which pass through a fixed point (4,6) is a circle. The radius of that circle is
View Solution

