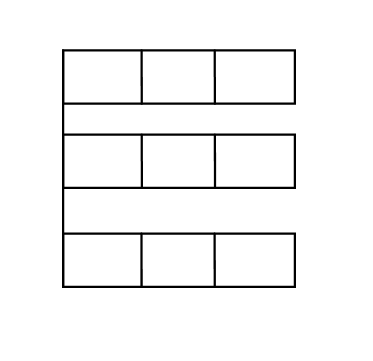
Find the number of ways in which letters A, A, A, B, B, B can be placed in the squares of the figure so that no row remains empty.

2nd and4th row block has to be selected.
One row out of 1st, 3rd and 5th will contain two letters and remaining one letter each.
Selection of one row that contains two letters is done in .3C1 ways.
Now two blocks can be selected from this row in .3C2 ways.
From each of reamaining two row, one blocks can be selected in .3C1 ways.
Hence total number of selections =.3C1×.3C2×.3C1×.3C1=81
In each selection of six places, letters A, A, A, B,B, B can be arranged in 6!3!3!=20
So, total number of ways =81×20=1620

Similar Questions
Find the number of ways in which the letters A, B, C, D, E, F can be placed in the 8 boxes of the given figure so that no row remains empty. (figure)
View SolutionFind the number of ways in which A A A B B B can be places in the square of figure as shown, so that no row remains empty is?
View SolutionThe number of ways in which the letters of the word PERSON can placed in the squares of the given figure so that no row remains empty is a. 24×6! b. 26×6! c. 26×7! d. 27×6!
View SolutionThe number of ways the letters of the word PERSON cann be placed in the squares of the figure shown so that no row remain empty is

View SolutionThe number of ways in which 5 X's can be placed in the squares of the figure so that no row remains empty is:
View SolutionIn how many ways the letters of the word DIPESH can be placed in the squares of the adjoining figure so that no row remains empty?

View SolutionNumber of ways in which the letters of the word "NATION" can be filled in the given figure such that no row remains empty and each box contains not more than one letter, are :

View SolutionThe number of ways in which four letters can be selected from the word degree, is
View SolutionThe number of ways in which five distinct objects can be put into three identical boxes so that no box remains empty is
View SolutionThe number of ways in which 5 letters can be placed in 5 marked envelopes, so that no letter is in the right encelope, is
View Solution