Question

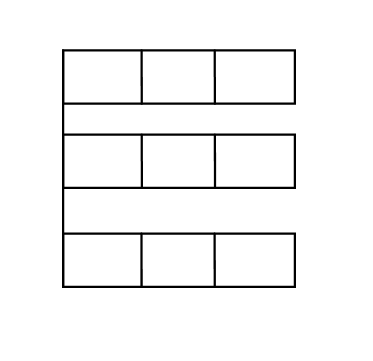
Find the number of ways in which the letters A, B, C, D, E, F can be placed in the 8 boxes of the given figure so that
no row remains empty.           
(figure)

Explanation

To solve the problem of arranging the letters A, B, C, D, E, and F in 8 boxes such that no row remains empty, we can follow these steps:

Step 1: Understand the Problem
We have 6 letters (A, B, C, D, E, F) and 8 boxes arranged in 3 rows. We need to ensure that each row has at least one letter.

Step 2: Determine Possible Distributions
We can distribute the letters in the following ways across the 3 rows:
1. Case 1: Row 1 gets 1 letter, Row 2 gets 3 letters, Row 3 gets 2 letters.
2. Case 2: Row 1 gets 1 letter, Row 2 gets 4 letters, Row 3 gets 1 letter.
3. Case 3: Row 1 gets 2 letters, Row 2 gets 3 letters, Row 3 gets 1 letter.
4. Case 4: Row 1 gets 2 letters, Row 2 gets 2 letters, Row 3 gets 2 letters.

Step 3: Calculate Arrangements for Each Case

Case 1: (1, 3, 2)
- Choose 1 letter for Row 1: \( \binom{6}{1} = 6 \)
- Choose 3 letters for Row 2 from the remaining 5 letters: \( \binom{5}{3} = 10 \)
- The remaining 2 letters go to Row 3: \( \binom{2}{2} = 1 \)
- Total arrangements for letters: \( 6! = 720 \)

Total for Case 1:
\( 6 \times 10 \times 1 \times 720 = 43200 \)

Case 2: (1, 4, 1)
- Choose 1 letter for Row 1: \( \binom{6}{1} = 6 \)
- Choose 4 letters for Row 2 from the remaining 5 letters: \( \binom{5}{4} = 5 \)
- The remaining 1 letter goes to Row 3: \( \binom{1}{1} = 1 \)
- Total arrangements for letters: \( 6! = 720 \)

Total for Case 2:
\( 6 \times 5 \times 1 \times 720 = 21600 \)

Case 3: (2, 3, 1)
- Choose 2 letters for Row 1: \( \binom{6}{2} = 15 \)
- Choose 3 letters for Row 2 from the remaining 4 letters: \( \binom{4}{3} = 4 \)
- The remaining 1 letter goes to Row 3: \( \binom{1}{1} = 1 \)
- Total arrangements for letters: \( 6! = 720 \)

Total for Case 3:
\( 15 \times 4 \times 1 \times 720 = 43200 \)

Case 4: (2, 2, 2)
- Choose 2 letters for Row 1: \( \binom{6}{2} = 15 \)
- Choose 2 letters for Row 2 from the remaining 4 letters: \( \binom{4}{2} = 6 \)
- The remaining 2 letters go to Row 3: \( \binom{2}{2} = 1 \)
- Total arrangements for letters: \( 6! = 720 \)

Total for Case 4:
\( 15 \times 6 \times 1 \times 720 = 64800 \)

Step 4: Sum All Cases
Now we add up all the cases:
\( 43200 + 21600 + 43200 + 64800 = 192000 \)

Final Answer
The total number of ways to arrange the letters A, B, C, D, E, and F in the 8 boxes such that no row remains empty is 192000.