Question

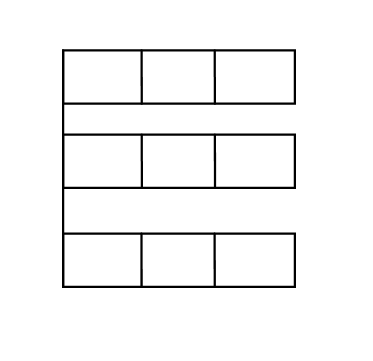
The number of ways in which the letters of the
word PERSON can placed in the squares of the given figure so that no row
remains empty is
a. $24\times 6!$
b. $26\times 6!$
c.
$26\times 7!$

d. $27\times 6!$

Explanation

To solve the problem of arranging the letters of the word "PERSON" in a way that no row remains empty, we will follow these steps:

1. Identify the Problem: We have 6 letters in the word "PERSON" and we need to arrange them in a figure with 3 rows (R1, R2, R3) such that no row is empty.

2. Determine the Distribution of Letters: Since we have 3 rows and 6 letters, we need to find all possible distributions of letters across the rows such that each row has at least one letter. The possible distributions are:
- 1 letter in R1, 1 letter in R2, and 4 letters in R3
- 1 letter in R1, 2 letters in R2, and 3 letters in R3
- 2 letters in R1, 1 letter in R2, and 3 letters in R3
- 2 letters in R1, 2 letters in R2, and 2 letters in R3

3. Calculate the Combinations for Each Distribution:
- For the distribution (1, 1, 4):
- Choose 1 letter from R1: \( \binom{2}{1} = 2 \)
- Choose 1 letter from R2: \( \binom{2}{1} = 2 \)
- Choose 4 letters from R3: \( \binom{4}{4} = 1 \)
- Total ways for this distribution: \( 2 \times 2 \times 1 = 4 \)

- For the distribution (1, 2, 3):
- Choose 1 letter from R1: \( \binom{2}{1} = 2 \)
- Choose 2 letters from R2: \( \binom{2}{2} = 1 \)
- Choose 3 letters from R3: \( \binom{4}{3} = 4 \)
- Total ways for this distribution: \( 2 \times 1 \times 4 = 8 \)

- For the distribution (2, 1, 3):
- Choose 2 letters from R1: \( \binom{2}{2} = 1 \)
- Choose 1 letter from R2: \( \binom{2}{1} = 2 \)
- Choose 3 letters from R3: \( \binom{4}{3} = 4 \)
- Total ways for this distribution: \( 1 \times 2 \times 4 = 8 \)

- For the distribution (2, 2, 2):
- Choose 2 letters from R1: \( \binom{2}{2} = 1 \)
- Choose 2 letters from R2: \( \binom{2}{2} = 1 \)
- Choose 2 letters from R3: \( \binom{4}{2} = 6 \)
- Total ways for this distribution: \( 1 \times 1 \times 6 = 6 \)

4. Sum the Total Combinations:
- Total combinations = \( 4 + 8 + 8 + 6 = 26 \)

5. Calculate the Arrangements of Letters:
- The total arrangements of the 6 letters in the word "PERSON" is \( 6! = 720 \).

6. Calculate the Final Result:
- The total number of ways to arrange the letters such that no row is empty is given by:
\( \text{Total Ways} = \text{Total Combinations} \times \text{Arrangements} = 26 \times 720 = 18720 \)

7. Identify the Correct Option:
- The required number of ways is \( 26 \times 6! \), which corresponds to option b.