The members of a chess club took part in a round robin competition in which each player plays with other once. All members scored the same number of points, except four juniors whose total score ere 17.5. How many members were there in the club? Assume that for each win a player scores 1 point, 1/2 for a draw, and zero for losing.
To solve the problem, let's break it down step by step:
Step 1: Understand the Problem
We have a chess club with a certain number of members who participate in a round-robin competition. Each player plays against every other player once. All members scored the same number of points except for four juniors whose total score is 17.5 points. We need to find the total number of members in the club.
Step 2: Define Variables
Let n be the total number of members in the chess club. Since each player plays against every other player, the total number of matches played is given by the combination formula (n2), which is equal to n(n−1)2.
Step 3: Calculate Total Points
In each match, the total points scored is always 1. This is because:
- If one player wins, they get 1 point and the other gets 0.
- If there is a draw, both players get 0.5 points each.
Thus, the total points scored in the tournament is equal to the total number of matches:
Total Points=(n2)=n(n−1)2
Step 4: Set Up the Equation
Let x be the score of each of the other n−4 members (since 4 juniors scored a total of 17.5 points). The total score of all members can then be expressed as:
Total Points=(n−4)x+17.5
Equating the two expressions for total points gives us:
n(n−1)2=(n−4)x+17.5
Step 5: Rearranging the Equation
Rearranging the equation, we get:
n(n−1)2−17.5=(n−4)x
Step 6: Simplifying
Multiply through by 2 to eliminate the fraction:
n(n−1)−35=2(n−4)x
This simplifies to:
n2−n−2(n−4)x=35
Step 7: Analyze Possible Values for x
Since x can be 0, 0.5, or 1 (as players can score 0, 0.5, or 1 point), we can analyze each case:
1. If x=1:
n2−n−2(n−4)=35⟹n2−n−2n+8=35⟹n2−3n−27=0
Solving this quadratic equation using the quadratic formula:
n=3±√32+4⋅272=3±√9+1082=3±√1172
Since √117 is not a perfect square, we discard this case.
2. If x=0.5:
n2−n−2(n−4)(0.5)=35⟹n2−n−(n−4)=35⟹n2−2n+4=35
Simplifying gives:
n2−2n−31=0
Solving this quadratic equation:
n=2±√(−2)2+4⋅312=2±√4+1242=2±√1282=2±8√22
Discarding non-integer values.
3. If x=0:
n2−n−2(n−4)(0)=35⟹n2−n=35⟹n2−n−35=0
Solving this quadratic equation:
n=1±√1+1402=1±√1412
Again, discard non-integer values.
Step 8: Final Calculation
From the analysis, we find that n−4 must be a divisor of 23 (since 23 is prime). The only possible values for n−4 are 1 or 23:
- If n−4=1, then n=5 (not valid as it leads to negative scores).
- If n−4=23, then n=27.
Conclusion
Thus, the total number of members in the chess club is:
27
We have a chess club with a certain number of members who participate in a round-robin competition. Each player plays against every other player once. All members scored the same number of points except for four juniors whose total score is 17.5 points. We need to find the total number of members in the club.
Let n be the total number of members in the chess club. Since each player plays against every other player, the total number of matches played is given by the combination formula (n2), which is equal to n(n−1)2.
In each match, the total points scored is always 1. This is because:
- If one player wins, they get 1 point and the other gets 0.
- If there is a draw, both players get 0.5 points each.
Total Points=(n2)=n(n−1)2
Let x be the score of each of the other n−4 members (since 4 juniors scored a total of 17.5 points). The total score of all members can then be expressed as:
Total Points=(n−4)x+17.5
Equating the two expressions for total points gives us:
n(n−1)2=(n−4)x+17.5
Rearranging the equation, we get:
n(n−1)2−17.5=(n−4)x
Multiply through by 2 to eliminate the fraction:
n(n−1)−35=2(n−4)x
This simplifies to:
n2−n−2(n−4)x=35
Since x can be 0, 0.5, or 1 (as players can score 0, 0.5, or 1 point), we can analyze each case:
n2−n−2(n−4)=35⟹n2−n−2n+8=35⟹n2−3n−27=0
Solving this quadratic equation using the quadratic formula:
n=3±√32+4⋅272=3±√9+1082=3±√1172
Since √117 is not a perfect square, we discard this case.
n2−n−2(n−4)(0.5)=35⟹n2−n−(n−4)=35⟹n2−2n+4=35
Simplifying gives:
n2−2n−31=0
Solving this quadratic equation:
n=2±√(−2)2+4⋅312=2±√4+1242=2±√1282=2±8√22
Discarding non-integer values.
n2−n−2(n−4)(0)=35⟹n2−n=35⟹n2−n−35=0
Solving this quadratic equation:
n=1±√1+1402=1±√1412
Again, discard non-integer values.
From the analysis, we find that n−4 must be a divisor of 23 (since 23 is prime). The only possible values for n−4 are 1 or 23:
- If n−4=1, then n=5 (not valid as it leads to negative scores).
- If n−4=23, then n=27.
Thus, the total number of members in the chess club is:
27
Similar Questions
In a shooting competition a man can score 5, 4, 3, 2, 1 or 0 points for each shot. Then the number of different ways in which he can score 10 in seven shots is
View Solution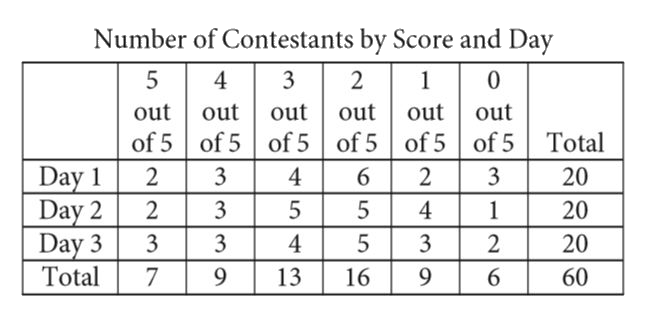
The same 20 contestants, on each of 3 days, answered 5 questions in order to win a prize. Each contestant received 1 point for each correct answer. The number of contestants receiving a given score on each day is shown in the table above.
No contestant received the same score on two different days. If a contestant is selected at random, what is the probability that the selected contestant received a score of 5 on Day 2 or Day 3, given that the contestant received a score of 5 on one of the three days?View Solution
Knowledge Check
- Question 1 - Select One
Thomas and Jonelle are playing darts in their garage using the board with the point value for each region shown below. The radius of the outside circle is 10 inches, and each of the other circles has a radius 2 inches smaller than the next larger circle. All of the circles have the same center. Thomas has only 1 dart left to throw and needs at least 30 points to win the game. Assuming that his last dart hits at a random point within a single region on the board, what is the percent chance that Thomas will win the game?
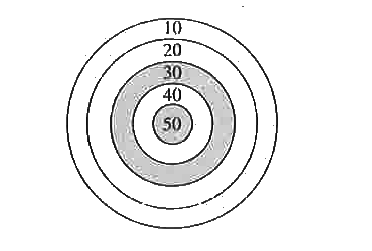 A36%B0.3C0.16D0.09
A36%B0.3C0.16D0.09 - Question 2 - Select One
The chemical formula of deoxyribonucleic acid
(DNA) is now well established. The molecule is a
very long chain, the backbone of which consists of a
regular alternation of sugar and phosphate groups.
5 To each sugar is attached a nitrogenous base, which
can be of four different types. Two of the possible
bases—adenine and guanine—are purines, and the
other two—thymine and cytosine—are pyrimidines.
So far as is known, the sequence of bases along the
10 chain is irregular. The monomer unit, consisting of
phosphate, sugar and base, is known as a nucleotide.
The first feature of our structure which is of
biological interest is that it consists not of one chain,
but of two. These two chains are both coiled around
15 a common fiber axis. It has often been assumed that
since there was only one chain in the chemical
formula there would only be one in the structural
unit. However, the density, taken with the X-ray
evidence, suggests very strongly that there are two.
20. The other biologically important feature is the
manner in which the two chains are held together.
This is done by hydrogen bonds between the bases.
The bases are joined together in pairs, a single base
from one chain being hydrogen-bonded to a single
25 base from the other. The important point is that only
certain pairs of bases will fit into the structure.
One member of a pair must be a purine and the other
a pyrimidine in order to bridge between the two
chains. If a pair consisted of two purines, for
30 example, there would not be room for it.
We believe that the bases will be present almost
entirely in their most probable forms. If this is true,
the conditions for forming hydrogen bonds are more
restrictive, and the only pairs of bases possible are:
35 adenine with thymine, and guanine with cytosine.
Adenine, for example, can occur on either chain, but
when it does, its partner on the other chain must
always be thymine.
The phosphate-sugar backbone of our model is
40 completely regular, but any sequence of the pairs of
bases can fit into the structure. It follows that in a
long molecule many different permutations are
possible, and it therefore seems likely that the precise
sequence of bases is the code which carries the
45 genetical information. If the actual order of the bases
on one of the pair of chains were given, one could
write down the exact order of the bases on the other
one, because of the specific pairing. Thus one chain
is, as it were, the complement of the other, and it is
50 this feature which suggests how the deoxyribonucleic
acid molecule might duplicate itself.
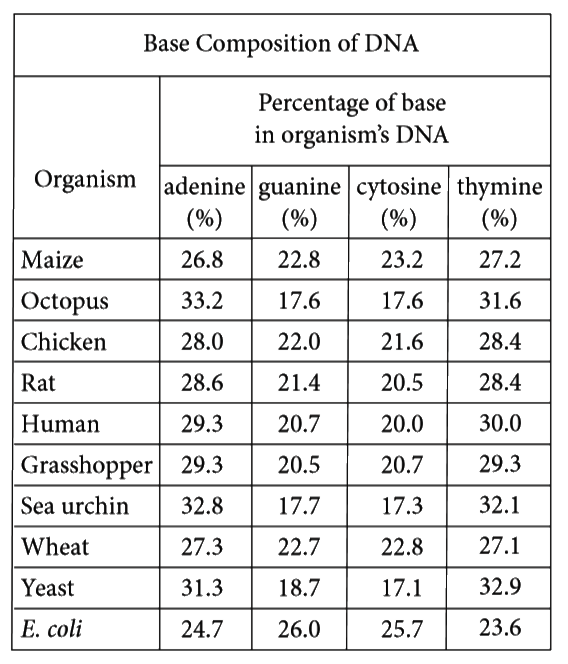
The table shows, for various organisms, the percentage of
each of the four types of nitrogenous bases in that
organism’s DNA.
Adapted from Manju Bansal, “DNA Structure: Revisiting the
Watson-Crick Double Helix.” ©2003 by Current Science Association,
Bangalore
31. Based on the table, is the percentage of adenine in each organism’s DNA the same or does it vary, and which statement made by the authors is most consistent with that data?AThe same, “Two of . . . pyrimidines” (lines 6-8)BThe same, “The important . . . structure” (lines 25-26)CIt varies, “Adenine . . . thymine” (lines 36-38)DIt varies, “It follows . . . information” (lines 41-45) - Question 3 - Select One
The chemical formula of deoxyribonucleic acid
(DNA) is now well established. The molecule is a
very long chain, the backbone of which consists of a
regular alternation of sugar and phosphate groups.
5 To each sugar is attached a nitrogenous base, which
can be of four different types. Two of the possible
bases—adenine and guanine—are purines, and the
other two—thymine and cytosine—are pyrimidines.
So far as is known, the sequence of bases along the
10 chain is irregular. The monomer unit, consisting of
phosphate, sugar and base, is known as a nucleotide.
The first feature of our structure which is of
biological interest is that it consists not of one chain,
but of two. These two chains are both coiled around
15 a common fiber axis. It has often been assumed that
since there was only one chain in the chemical
formula there would only be one in the structural
unit. However, the density, taken with the X-ray
evidence, suggests very strongly that there are two.
20. The other biologically important feature is the
manner in which the two chains are held together.
This is done by hydrogen bonds between the bases.
The bases are joined together in pairs, a single base
from one chain being hydrogen-bonded to a single
25 base from the other. The important point is that only
certain pairs of bases will fit into the structure.
One member of a pair must be a purine and the other
a pyrimidine in order to bridge between the two
chains. If a pair consisted of two purines, for
30 example, there would not be room for it.
We believe that the bases will be present almost
entirely in their most probable forms. If this is true,
the conditions for forming hydrogen bonds are more
restrictive, and the only pairs of bases possible are:
35 adenine with thymine, and guanine with cytosine.
Adenine, for example, can occur on either chain, but
when it does, its partner on the other chain must
always be thymine.
The phosphate-sugar backbone of our model is
40 completely regular, but any sequence of the pairs of
bases can fit into the structure. It follows that in a
long molecule many different permutations are
possible, and it therefore seems likely that the precise
sequence of bases is the code which carries the
45 genetical information. If the actual order of the bases
on one of the pair of chains were given, one could
write down the exact order of the bases on the other
one, because of the specific pairing. Thus one chain
is, as it were, the complement of the other, and it is
50 this feature which suggests how the deoxyribonucleic
acid molecule might duplicate itself.
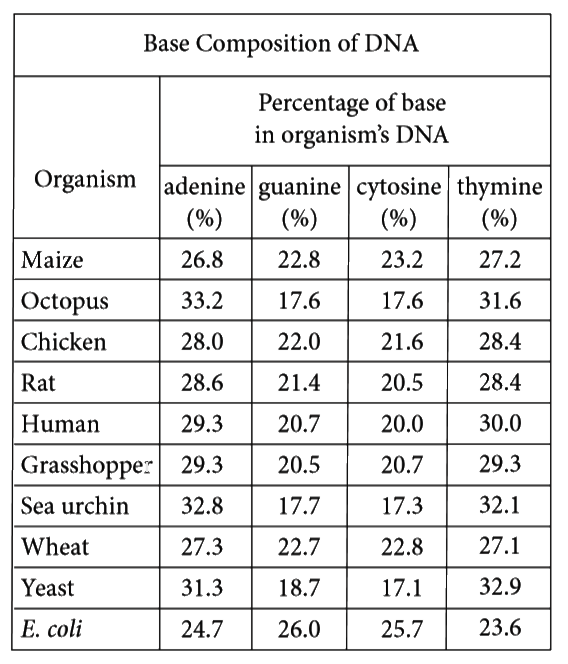
The table shows, for various organisms, the percentage of
each of the four types of nitrogenous bases in that
organism’s DNA.
Adapted from Manju Bansal, “DNA Structure: Revisiting the
Watson-Crick Double Helix.” ©2003 by Current Science Association,
Bangalore
23. A student claims that nitrogenous bases pair randomly with one another. Which of the following statements in the passage contradicts the student’s claim?ALines 5-6 (“To each . . . types”)BLines 9-10 (“So far . . . irregular”)CLines 23-25 (“The bases . . . other”)DLines 27-29 (“One member . . . chains”)
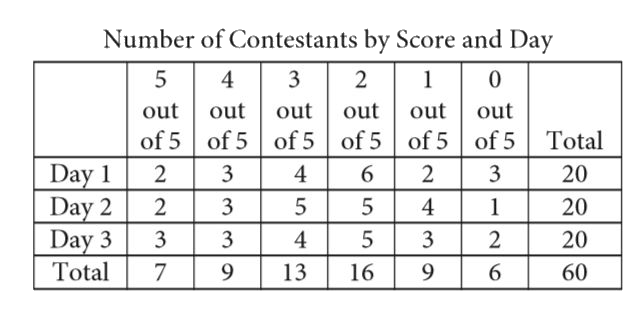
The same 20 contestants, on each of 3 days, answered 5 questions in order to win a prize. Each contestant received 1 point for each correct answer. The number of contestants receiving a given score on each day is shown in the table above.
What was the mean score of the contestants on Day 1 ?View SolutionThe chemical formula of deoxyribonucleic acid
(DNA) is now well established. The molecule is a
very long chain, the backbone of which consists of a
regular alternation of sugar and phosphate groups.
5 To each sugar is attached a nitrogenous base, which
can be of four different types. Two of the possible
bases—adenine and guanine—are purines, and the
other two—thymine and cytosine—are pyrimidines.
So far as is known, the sequence of bases along the
10 chain is irregular. The monomer unit, consisting of
phosphate, sugar and base, is known as a nucleotide.
The first feature of our structure which is of
biological interest is that it consists not of one chain,
but of two. These two chains are both coiled around
15 a common fiber axis. It has often been assumed that
since there was only one chain in the chemical
formula there would only be one in the structural
unit. However, the density, taken with the X-ray
evidence, suggests very strongly that there are two.
20. The other biologically important feature is the
manner in which the two chains are held together.
This is done by hydrogen bonds between the bases.
The bases are joined together in pairs, a single base
from one chain being hydrogen-bonded to a single
25 base from the other. The important point is that only
certain pairs of bases will fit into the structure.
One member of a pair must be a purine and the other
a pyrimidine in order to bridge between the two
chains. If a pair consisted of two purines, for
30 example, there would not be room for it.
We believe that the bases will be present almost
entirely in their most probable forms. If this is true,
the conditions for forming hydrogen bonds are more
restrictive, and the only pairs of bases possible are:
35 adenine with thymine, and guanine with cytosine.
Adenine, for example, can occur on either chain, but
when it does, its partner on the other chain must
always be thymine.
The phosphate-sugar backbone of our model is
40 completely regular, but any sequence of the pairs of
bases can fit into the structure. It follows that in a
long molecule many different permutations are
possible, and it therefore seems likely that the precise
sequence of bases is the code which carries the
45 genetical information. If the actual order of the bases
on one of the pair of chains were given, one could
write down the exact order of the bases on the other
one, because of the specific pairing. Thus one chain
is, as it were, the complement of the other, and it is
50 this feature which suggests how the deoxyribonucleic
acid molecule might duplicate itself.
The table shows, for various organisms, the percentage of
each of the four types of nitrogenous bases in that
organism’s DNA.
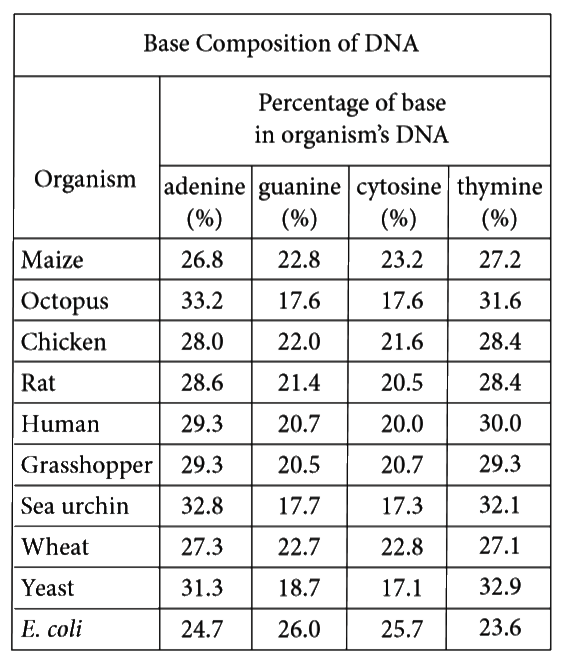
Adapted from Manju Bansal, “DNA Structure: Revisiting the
Watson-Crick Double Helix.” ©2003 by Current Science Association,
Bangalore
26. Based on the passage, the authors’ statement “If a pair consisted of two purines, for example, there would not be room for it” (lines 29-30) implies that a pairView SolutionThe chemical formula of deoxyribonucleic acid
(DNA) is now well established. The molecule is a
very long chain, the backbone of which consists of a
regular alternation of sugar and phosphate groups.
5 To each sugar is attached a nitrogenous base, which
can be of four different types. Two of the possible
bases—adenine and guanine—are purines, and the
other two—thymine and cytosine—are pyrimidines.
So far as is known, the sequence of bases along the
10 chain is irregular. The monomer unit, consisting of
phosphate, sugar and base, is known as a nucleotide.
The first feature of our structure which is of
biological interest is that it consists not of one chain,
but of two. These two chains are both coiled around
15 a common fiber axis. It has often been assumed that
since there was only one chain in the chemical
formula there would only be one in the structural
unit. However, the density, taken with the X-ray
evidence, suggests very strongly that there are two.
20. The other biologically important feature is the
manner in which the two chains are held together.
This is done by hydrogen bonds between the bases.
The bases are joined together in pairs, a single base
from one chain being hydrogen-bonded to a single
25 base from the other. The important point is that only
certain pairs of bases will fit into the structure.
One member of a pair must be a purine and the other
a pyrimidine in order to bridge between the two
chains. If a pair consisted of two purines, for
30 example, there would not be room for it.
We believe that the bases will be present almost
entirely in their most probable forms. If this is true,
the conditions for forming hydrogen bonds are more
restrictive, and the only pairs of bases possible are:
35 adenine with thymine, and guanine with cytosine.
Adenine, for example, can occur on either chain, but
when it does, its partner on the other chain must
always be thymine.
The phosphate-sugar backbone of our model is
40 completely regular, but any sequence of the pairs of
bases can fit into the structure. It follows that in a
long molecule many different permutations are
possible, and it therefore seems likely that the precise
sequence of bases is the code which carries the
45 genetical information. If the actual order of the bases
on one of the pair of chains were given, one could
write down the exact order of the bases on the other
one, because of the specific pairing. Thus one chain
is, as it were, the complement of the other, and it is
50 this feature which suggests how the deoxyribonucleic
acid molecule might duplicate itself.
The table shows, for various organisms, the percentage of
each of the four types of nitrogenous bases in that
organism’s DNA.

Adapted from Manju Bansal, “DNA Structure: Revisiting the
Watson-Crick Double Helix.” ©2003 by Current Science Association,
Bangalore
24. In the second paragraph (lines 12-19), what do the authors claim to be a feature of biological interest?View SolutionThe chemical formula of deoxyribonucleic acid
(DNA) is now well established. The molecule is a
very long chain, the backbone of which consists of a
regular alternation of sugar and phosphate groups.
5 To each sugar is attached a nitrogenous base, which
can be of four different types. Two of the possible
bases—adenine and guanine—are purines, and the
other two—thymine and cytosine—are pyrimidines.
So far as is known, the sequence of bases along the
10 chain is irregular. The monomer unit, consisting of
phosphate, sugar and base, is known as a nucleotide.
The first feature of our structure which is of
biological interest is that it consists not of one chain,
but of two. These two chains are both coiled around
15 a common fiber axis. It has often been assumed that
since there was only one chain in the chemical
formula there would only be one in the structural
unit. However, the density, taken with the X-ray
evidence, suggests very strongly that there are two.
20. The other biologically important feature is the
manner in which the two chains are held together.
This is done by hydrogen bonds between the bases.
The bases are joined together in pairs, a single base
from one chain being hydrogen-bonded to a single
25 base from the other. The important point is that only
certain pairs of bases will fit into the structure.
One member of a pair must be a purine and the other
a pyrimidine in order to bridge between the two
chains. If a pair consisted of two purines, for
30 example, there would not be room for it.
We believe that the bases will be present almost
entirely in their most probable forms. If this is true,
the conditions for forming hydrogen bonds are more
restrictive, and the only pairs of bases possible are:
35 adenine with thymine, and guanine with cytosine.
Adenine, for example, can occur on either chain, but
when it does, its partner on the other chain must
always be thymine.
The phosphate-sugar backbone of our model is
40 completely regular, but any sequence of the pairs of
bases can fit into the structure. It follows that in a
long molecule many different permutations are
possible, and it therefore seems likely that the precise
sequence of bases is the code which carries the
45 genetical information. If the actual order of the bases
on one of the pair of chains were given, one could
write down the exact order of the bases on the other
one, because of the specific pairing. Thus one chain
is, as it were, the complement of the other, and it is
50 this feature which suggests how the deoxyribonucleic
acid molecule might duplicate itself.
The table shows, for various organisms, the percentage of
each of the four types of nitrogenous bases in that
organism’s DNA.

Adapted from Manju Bansal, “DNA Structure: Revisiting the
Watson-Crick Double Helix.” ©2003 by Current Science Association,
Bangalore
25. The authors’ main purpose of including the information about X-ray evidence and density is toView SolutionThe chemical formula of deoxyribonucleic acid
(DNA) is now well established. The molecule is a
very long chain, the backbone of which consists of a
regular alternation of sugar and phosphate groups.
5 To each sugar is attached a nitrogenous base, which
can be of four different types. Two of the possible
bases—adenine and guanine—are purines, and the
other two—thymine and cytosine—are pyrimidines.
So far as is known, the sequence of bases along the
10 chain is irregular. The monomer unit, consisting of
phosphate, sugar and base, is known as a nucleotide.
The first feature of our structure which is of
biological interest is that it consists not of one chain,
but of two. These two chains are both coiled around
15 a common fiber axis. It has often been assumed that
since there was only one chain in the chemical
formula there would only be one in the structural
unit. However, the density, taken with the X-ray
evidence, suggests very strongly that there are two.
20. The other biologically important feature is the
manner in which the two chains are held together.
This is done by hydrogen bonds between the bases.
The bases are joined together in pairs, a single base
from one chain being hydrogen-bonded to a single
25 base from the other. The important point is that only
certain pairs of bases will fit into the structure.
One member of a pair must be a purine and the other
a pyrimidine in order to bridge between the two
chains. If a pair consisted of two purines, for
30 example, there would not be room for it.
We believe that the bases will be present almost
entirely in their most probable forms. If this is true,
the conditions for forming hydrogen bonds are more
restrictive, and the only pairs of bases possible are:
35 adenine with thymine, and guanine with cytosine.
Adenine, for example, can occur on either chain, but
when it does, its partner on the other chain must
always be thymine.
The phosphate-sugar backbone of our model is
40 completely regular, but any sequence of the pairs of
bases can fit into the structure. It follows that in a
long molecule many different permutations are
possible, and it therefore seems likely that the precise
sequence of bases is the code which carries the
45 genetical information. If the actual order of the bases
on one of the pair of chains were given, one could
write down the exact order of the bases on the other
one, because of the specific pairing. Thus one chain
is, as it were, the complement of the other, and it is
50 this feature which suggests how the deoxyribonucleic
acid molecule might duplicate itself.
The table shows, for various organisms, the percentage of
each of the four types of nitrogenous bases in that
organism’s DNA.
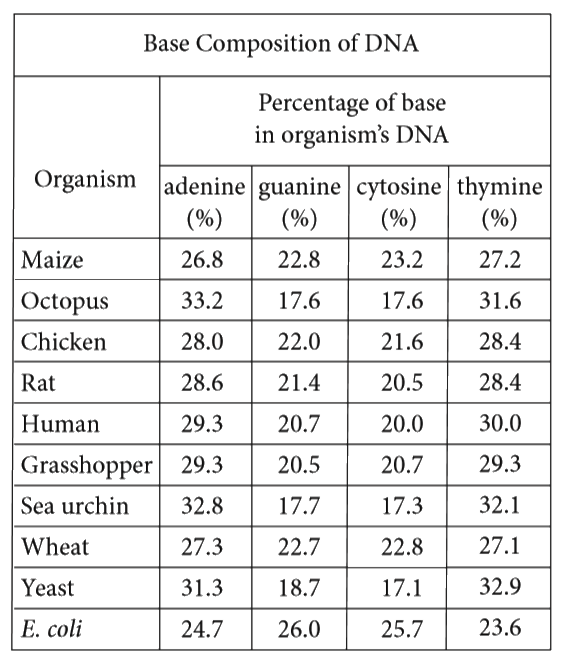
Adapted from Manju Bansal, “DNA Structure: Revisiting the
Watson-Crick Double Helix.” ©2003 by Current Science Association,
Bangalor
27. The authors’ use of the words “exact,” “specific,” and “complement” in lines 47-49 in the final paragraph functions mainly toView Solution

