Two cyclists start from the junction of two perpendicular roads, there velocities being 3um/m∈ and 4um/m∈ , respectively. Find the rate at which the two cyclists separate.
The correct Answer is:5u
To solve the problem, we need to find the rate at which the two cyclists are separating after they start from a junction of two perpendicular roads. Let's break down the solution step by step.
Step 1: Understand the Problem
We have two cyclists starting from the same point (the junction) and moving in perpendicular directions. One cyclist travels at a speed of 3u m/min, and the other at 4u m/min. We want to find the rate at which the distance between them is increasing.
Step 2: Define Variables
Let:
- t = time in minutes
- Distance covered by the first cyclist after time t = d1=3u⋅t
- Distance covered by the second cyclist after time t = d2=4u⋅t
Step 3: Use Pythagorean Theorem
Since the cyclists are moving in perpendicular directions, we can use the Pythagorean theorem to find the distance x between them:
x2=d21+d22
Substituting the distances:
x2=(3u⋅t)2+(4u⋅t)2
x2=9u2t2+16u2t2
x2=25u2t2
Taking the square root:
x=5u⋅t
Step 4: Differentiate with Respect to Time
To find the rate at which the distance x is increasing, we differentiate x with respect to t:
dxdt=ddt(5u⋅t)
dxdt=5u
Step 5: Conclusion
The rate at which the two cyclists are separating is 5u m/min.
We have two cyclists starting from the same point (the junction) and moving in perpendicular directions. One cyclist travels at a speed of 3u m/min, and the other at 4u m/min. We want to find the rate at which the distance between them is increasing.
Let:
- t = time in minutes
- Distance covered by the first cyclist after time t = d1=3u⋅t
- Distance covered by the second cyclist after time t = d2=4u⋅t
Since the cyclists are moving in perpendicular directions, we can use the Pythagorean theorem to find the distance x between them:
x2=d21+d22
Substituting the distances:
x2=(3u⋅t)2+(4u⋅t)2
x2=9u2t2+16u2t2
x2=25u2t2
Taking the square root:
x=5u⋅t
To find the rate at which the distance x is increasing, we differentiate x with respect to t:
dxdt=ddt(5u⋅t)
dxdt=5u
The rate at which the two cyclists are separating is 5u m/min.
Topper's Solved these Questions
- APPLICATION OF DERIVATIVESBOOK - CENGAGE ENGLISHCHAPTER - APPLICATION OF DERIVATIVESEXERCISE - CONCEPT APPLICATION EXERCISE 5.6
5 Videos
- APPLICATION OF DERIVATIVESBOOK - CENGAGE ENGLISHCHAPTER - APPLICATION OF DERIVATIVESEXERCISE - CONCEPT APPLICATION EXERCISE 5.7
8 Videos
- APPLICATION OF DERIVATIVESBOOK - CENGAGE ENGLISHCHAPTER - APPLICATION OF DERIVATIVESEXERCISE - CONCEPT APPLICATION EXERCISE 5.4
6 Videos
- 3D COORDINATION SYSTEM BOOK - CENGAGE ENGLISHCHAPTER - 3D COORDINATION SYSTEM EXERCISE - DPP 3.1
11 Videos
- APPLICATION OF INTEGRALSBOOK - CENGAGE ENGLISHCHAPTER - APPLICATION OF INTEGRALSEXERCISE - All Questions
142 Videos
Similar Questions
Two men A and B start with velocities v at the same time from the junction of two roads inclined at 45∘ to each other.If they travel by different roads,find the rate at which they are being separated.
View SolutionTwo men PandQ start with velocity u at the same time from the junction of two roads inclined at 450 to each other. If they travel by different roads, find the rate at which they are being separated.
View SolutionTwo men PandQ start with velocity u at the same time from the junction of two roads inclined at 450 to each other. If they travel by different roads, find the rate at which they are being separated.
View SolutionTwo men PandQ start with velocity u at the same time from the junction of two roads inclined at 450 to each other. If they travel by different roads, find the rate at which they are being separated.
View SolutionA body of mass M at rest explodes into three pieces, two of which of mass M//4 each are thrown off in perpendicular directions eith velocities of 3m/s and 4m/s respectively. The third piece will be thrown off with a velocity of
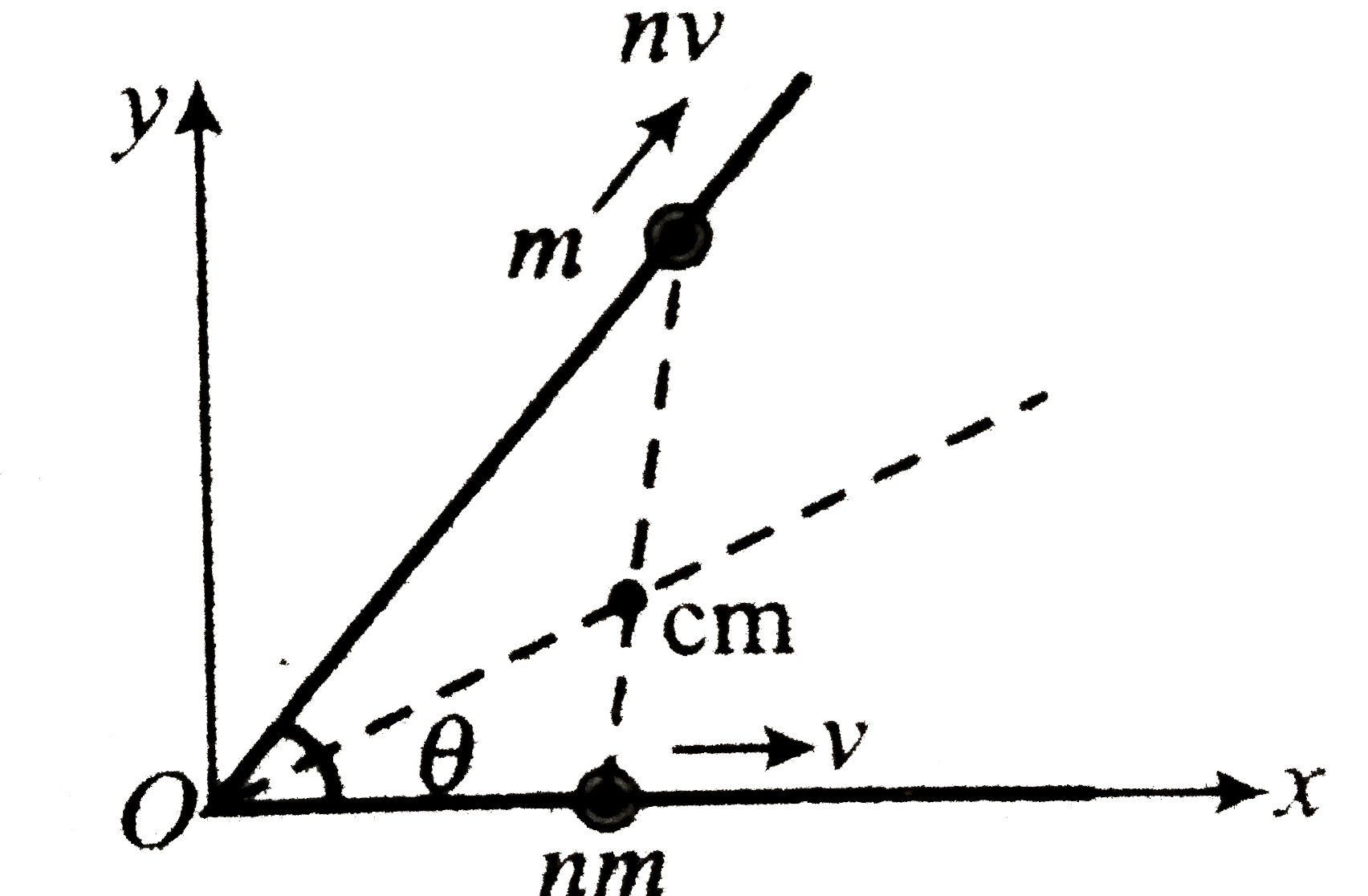
View SolutionTwo masses nm and m, start simultaneously from the intersection of two straight lines with velocities v and nv respectively. It is observed that the path of their centre of mass is a straight line bisecting the angle between the given straight lines. Find the magnitude of the velocity of centre of mass. [Here θ=angle between the lines]
View SolutionThe distance of the two planets from the Sun are 1013m and 1012m, respectively. Find the ratio of time periods of the two planets.
View SolutionTwo particles are projected from a tower horizontally in opposite directions with velocities 10m/sand20m/s. Find the time when their velocity vectors are mutually perpendicular. Take g=10m/s2.
View SolutionTwo particles P and Q simultaneously start moving from point A with velocities 15m/s and 20m/s respectively. The two particles move with acceleration equal in magnitude but opposite in direction. When P overtakes Q at point B then its velocity is 30m/s, the velocity of Q at point B will be
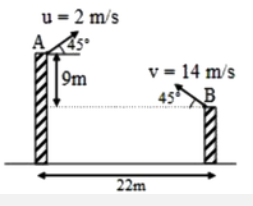
View SolutionTwo particles are simultaneously thrown from the top of two towards as shown. Their velocities are 2ms−1and14ms−1. Horizontal and vertical separations between these particles are 22 m and 9 m respectively. Then the minimum separation between the particles in the process of their motion in meters is (g=10ms−2)
View Solution
