Two men PandQ start with velocity u at the same time from the junction of two roads inclined at 450 to each other. If they travel by different roads, find the rate at which they are being separated.
The correct Answer is:u√(2−√2)
To solve the problem, we need to find the rate at which two men, P and Q, are separating as they travel along two roads inclined at an angle of 45∘ to each other, both starting from the same point with the same velocity u.
1. Understanding the Geometry:
- Let O be the junction where both men start.
- Let P travel along one road and Q travel along the other road.
- The angle between the two roads is 45∘.
2. Setting Up the Variables:
- Let x be the distance traveled by each man after time t.
- Since both men travel with the same velocity u, the distance x can be expressed as:
x=ut
- Let y be the distance between the two men after time t.
3. Using the Law of Cosines:
- According to the law of cosines, for the triangle formed by the points O, P, and Q:
y2=x2+x2−2x2cos(45∘)
- Since cos(45∘)=1√2, we can substitute this into the equation:
y2=2x2−2x2⋅1√2
- Simplifying this gives:
y2=2x2(1−1√2)
4. Simplifying Further:
- Let’s factor out x2:
y2=2x2(1−1√2)
- We can express y as:
y=x
⎷2(1−1√2)
5. Finding the Rate of Change:
- To find dydt, we differentiate both sides with respect to t:
dydt=
⎷2(1−1√2)⋅dxdt
- Since x=ut, we have dxdt=u:
dydt=
⎷2(1−1√2)⋅u
6. Final Calculation:
- We can calculate 1−1√2=√2−1√2, so:
dydt=u√2⋅√2−1√2=u√2(√2−1)
Final Result:
The rate at which the two men are separating is given by:
dydt=u√2(√2−1)
- Let O be the junction where both men start.
- Let P travel along one road and Q travel along the other road.
- The angle between the two roads is 45∘.
- Let x be the distance traveled by each man after time t.
- Since both men travel with the same velocity u, the distance x can be expressed as:
x=ut
- Let y be the distance between the two men after time t.
- According to the law of cosines, for the triangle formed by the points O, P, and Q:
y2=x2+x2−2x2cos(45∘)
- Since cos(45∘)=1√2, we can substitute this into the equation:
y2=2x2−2x2⋅1√2
- Simplifying this gives:
y2=2x2(1−1√2)
- Let’s factor out x2:
y2=2x2(1−1√2)
- We can express y as:
y=x
⎷2(1−1√2)
- To find dydt, we differentiate both sides with respect to t:
dydt=
⎷2(1−1√2)⋅dxdt
- Since x=ut, we have dxdt=u:
dydt=
⎷2(1−1√2)⋅u
- We can calculate 1−1√2=√2−1√2, so:
dydt=u√2⋅√2−1√2=u√2(√2−1)
The rate at which the two men are separating is given by:
dydt=u√2(√2−1)
Topper's Solved these Questions
- BOOK - CENGAGE ENGLISHCHAPTER - APPLICATION OF DERIVATIVESEXERCISE - CONCEPT APPLICATION EXERCISE 5.65videos
APPLICATION OF DERIVATIVES
- BOOK - CENGAGE ENGLISHCHAPTER - APPLICATION OF DERIVATIVESEXERCISE - CONCEPT APPLICATION EXERCISE 5.78videos
APPLICATION OF DERIVATIVES
- BOOK - CENGAGE ENGLISHCHAPTER - APPLICATION OF DERIVATIVESEXERCISE - CONCEPT APPLICATION EXERCISE 5.46videos
APPLICATION OF DERIVATIVES
- BOOK - CENGAGE ENGLISHCHAPTER - 3D COORDINATION SYSTEM EXERCISE - DPP 3.111videos
3D COORDINATION SYSTEM
- BOOK - CENGAGE ENGLISHCHAPTER - APPLICATION OF INTEGRALSEXERCISE - All Questions142videos
APPLICATION OF INTEGRALS
Similar Questions
Two men A and B start with velocities v at the same time from the junction of two roads inclined at 45∘ to each other.If they travel by different roads,find the rate at which they are being separated.
View SolutionTwo cyclists start from the junction of two perpendicular roads, there velocities being 3um/m∈ and 4um/m∈ , respectively. Find the rate at which the two cyclists separate.
View SolutionTwo cyclists start from the junction of two perpendicular roads, there velocities being 3um/m∈ and 4um/m∈ , respectively. Find the rate at which the two cyclists separate.
View SolutionThe distance between two particles is decreasing at the rate of 6 m/sec,when they travel in opposite direction to each other. If these particles travel with same speeds and in the same direction, then the separation increase at the rate of 4 m/sec. The particles have speed as
View SolutionPlaces A and B are 100 km apart on a highway. One car starts from A and another from b at the same time. If the cars travel in the same direction at different speeds, they meet in 5 hours. If they travel towards each other, they meet in 1 hour. What are the speeds of the two cars
View SolutionPlaces A and B are 100 km apart on a highway. One car starts from A and another from b at the same time. If the cars travel in the same direction at different speeds, they meet in 5 hours. If they travel towards each other, they meet in 1 hour. What are the speeds of the two cars
View SolutionTwo ships leave port at the same time. One goes 24 km per hour in the direction N 450E and other travels 32 km per hour in the direction S750E. Find the distance between the ships at the end of 3 hours.
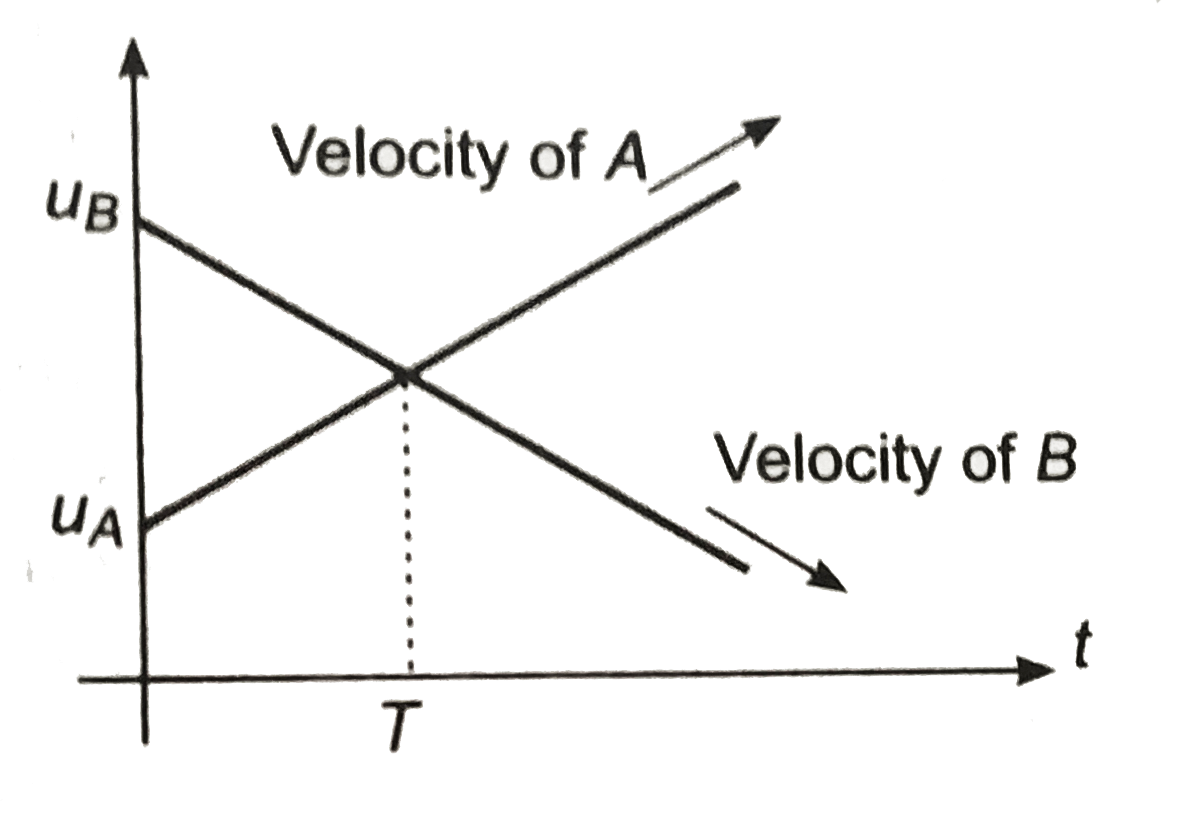
View SolutionA situation is shown in which two objects A and B start their motion from same point in same direction. The graph of their velocities against time is drawn. uAanduB are the initial velocities of A and B respectively. T is the time at which their velocities become equal after start of motion. You cannot use the data of one question while solving another question of the same set. So all the questions are independent of each other.
5. If the value of T is 4 s, then the time after which A will meet B is
 View Solution
View SolutionTwo particles P1 and P2 are performing SHM along the same line about the same mean position , initial they are at their extreme position. If the time period of each particle is 12 sec and the difference of their amplitude is 12cm then find the minimum time after which the separation between the particle becomes 6cm.
View SolutionThrough a rectangular field of sides 90 m × 60 m , two roads are constructed which are parallel to the sides and cut each other at right angles through the centre of the field. If the width of the roads is 3 m, find the total area covered by the two roads.
View Solution

