Question

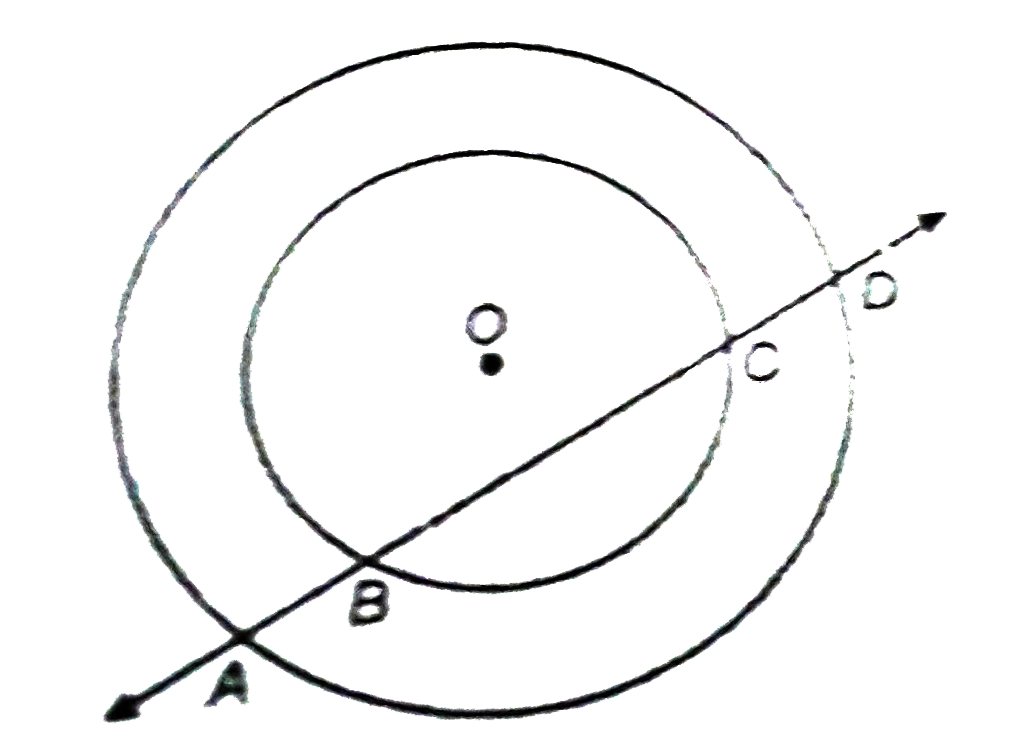
In Figure, $l$
is a line
intersecting the two concentric circles, whose common centre is $O,$
at the
points $A,B,CandD$
. Show that
$AB=CD\stackrel{.}{}$

Explanation

To solve the problem, we need to show that $$AB=CD$$ where $$l$$ is a line intersecting two concentric circles at points $$A,B,C,$$ and $$D$$ with a common center $$O$$.

1. Identify the Given Information:
- We have two concentric circles with center \( O \).
- The line \( l \) intersects the outer circle at points \( A \) and \( D \) and the inner circle at points \( B \) and \( C \).

2. Establish Radii:
- Let \( r_1 \) be the radius of the outer circle (i.e., \( OA = OD \)).
- Let \( r_2 \) be the radius of the inner circle (i.e., \( OB = OC \)).
- Since both circles are concentric, we have \( OA = OD \) and \( OB = OC \).

3. Angles in the Triangles:
- Consider triangles \( OAB \) and \( OCD \).
- Since \( OB = OC \) (radii of the inner circle), we can state that \( \angle OAB = \angle OCD \) because they subtend the same arc \( AB \) and \( CD \) respectively.

4. Using Congruence of Triangles:
- We have:
- \( OA = OD \) (radii of the outer circle)
- \( OB = OC \) (radii of the inner circle)
- \( \angle OAB = \angle OCD \) (as established)
- Therefore, by the Side-Angle-Side (SAS) congruence criterion, triangles \( OAB \) and \( OCD \) are congruent.

5. Conclusion from Congruence:
- Since triangles \( OAB \) and \( OCD \) are congruent, their corresponding sides are equal.
- Thus, we conclude that \( AB = CD \).

Final Statement:
Therefore, we have shown that \( AB = CD \).

---