The circumference of a circle exceeds the diameter by 16.8 cm. Find the circumference of the circle.
To solve the problem step by step, we will use the relationship between the circumference and diameter of a circle.
Step 1: Define the variables
Let the radius of the circle be r. The diameter d of the circle can be expressed as:
d=2r
Step 2: Write the formula for circumference
The circumference C of the circle is given by the formula:
C=2πr
Step 3: Set up the equation based on the problem statement
According to the problem, the circumference exceeds the diameter by 16.8 cm. Therefore, we can write the equation as:
C=d+16.8
Substituting the expressions for C and d:
2πr=2r+16.8
Step 4: Rearrange the equation
We can rearrange the equation to isolate terms involving r:
2πr−2r=16.8
Factoring out r from the left side gives:
r(2π−2)=16.8
Step 5: Solve for r
Now, we can solve for r:
r=16.82π−2
Step 6: Calculate the value of r
Using the approximate value of π≈3.14:
r=16.82(3.14)−2=16.86.28−2=16.84.28≈3.92 cm
Step 7: Find the circumference
Now that we have r, we can find the circumference:
C=2πr=2π(3.92)
Calculating this gives:
C≈2×3.14×3.92≈24.63 cm
Final Answer
The circumference of the circle is approximately 24.63 cm.
---
Let the radius of the circle be r. The diameter d of the circle can be expressed as:
d=2r
The circumference C of the circle is given by the formula:
C=2πr
According to the problem, the circumference exceeds the diameter by 16.8 cm. Therefore, we can write the equation as:
C=d+16.8
Substituting the expressions for C and d:
2πr=2r+16.8
We can rearrange the equation to isolate terms involving r:
2πr−2r=16.8
Factoring out r from the left side gives:
r(2π−2)=16.8
Now, we can solve for r:
r=16.82π−2
Using the approximate value of π≈3.14:
r=16.82(3.14)−2=16.86.28−2=16.84.28≈3.92 cm
Now that we have r, we can find the circumference:
C=2πr=2π(3.92)
Calculating this gives:
C≈2×3.14×3.92≈24.63 cm
The circumference of the circle is approximately 24.63 cm.
Topper's Solved these Questions
Similar Questions
Knowledge Check
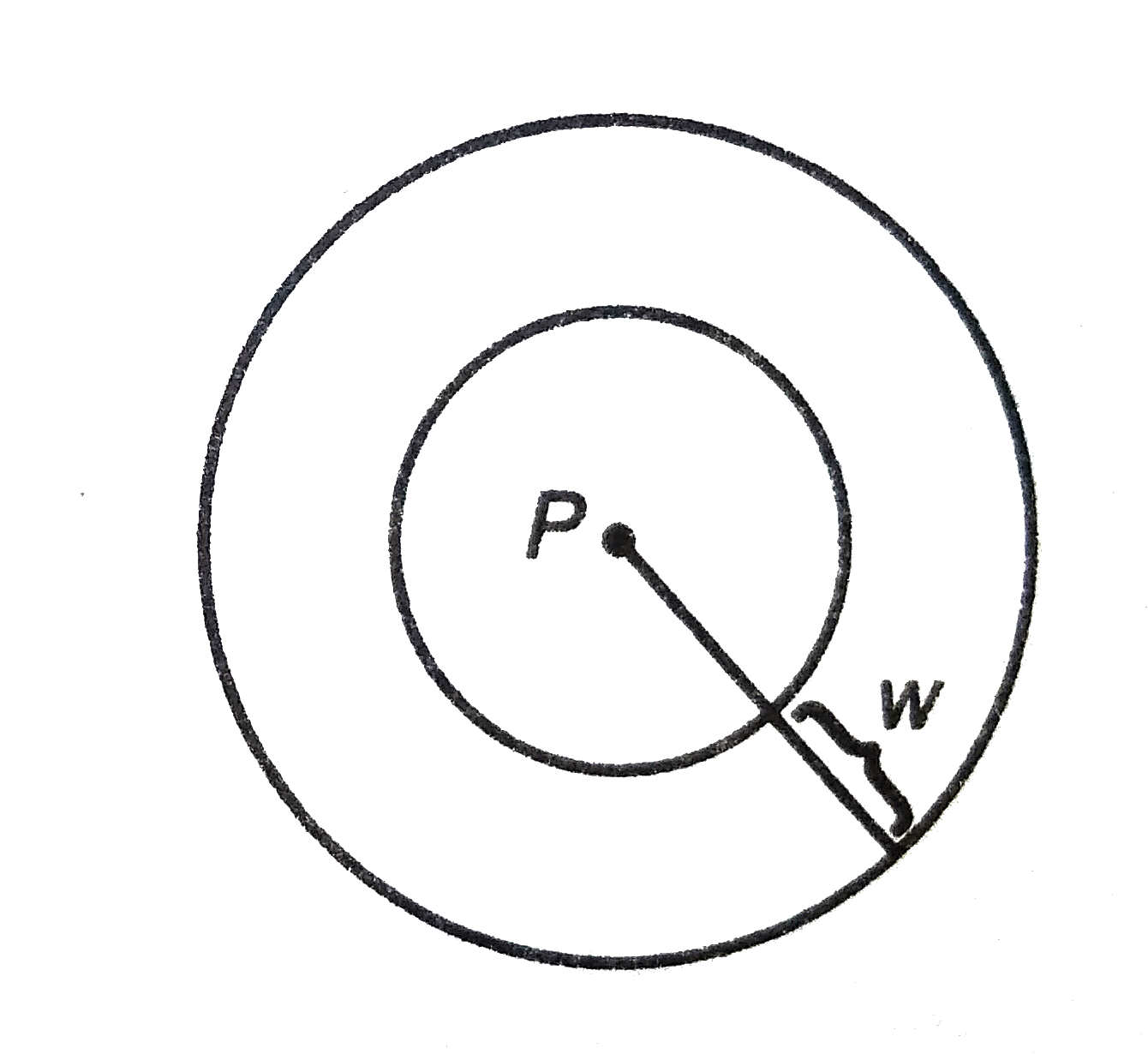
In the figure above, point P is the center of each circle. The circumference of the larger circle exceeds the circumference of the smaller circle by 12π. What is the width, w, of the region between the two circles?A4B6C8D9
The circumference of a circle exceeds its diameter by 270 cm. Find its diameter.
View SolutionFind the circumference of a circle whose diameter is 42 cm.
View SolutionThe circumference of a circle is 17π. What is the diameter?
View SolutionA rhombus has the same perimeter as the circumference of a circle. If the side of the rhombus is 2.2 m. find the radius of the circle.
View SolutionThe circumference of a circle is 44 cm. Find its area.
View SolutionThe circumference of a circle is 3.14 m, find its area.
View SolutionThe sum of diameter of two circles is 14 cm and the difference of their circumferences is 8 cm. Find the circumference of two circles
View Solution
