In the trapezium ABCD,AC and BD intersect at O and also AB=2CD If the area of AOB=84cm2, find the area of COD.
To solve the problem step by step, we will use the properties of similar triangles and the relationship between the areas of triangles formed by the intersection of diagonals in a trapezium.
1. Understanding the Given Information:
- We have a trapezium ABCD where AC and BD intersect at point O.
- It is given that AB = 2CD.
- The area of triangle AOB is given as 84 cm².
2. Drawing the Diagram:
- Draw trapezium ABCD with AB and CD as the parallel sides.
- Mark the intersection point O where diagonals AC and BD meet.
3. Identifying Angles:
- Since O is the intersection of diagonals, the angles ∠AOB and ∠COD are vertically opposite angles and are equal.
- The angles ∠OAB and ∠OCD are alternate angles, which are also equal.
4. Establishing Similarity:
- From the above angle relationships, we can conclude that triangles AOB and COD are similar (by AA criterion of similarity).
- Therefore, the ratio of their corresponding sides is equal.
5. Setting Up the Ratio:
- Let CD = x. Then, AB = 2x (since AB = 2CD).
- The ratio of the sides is:
ABCD=2xx=2
- Let OE be the height from O to AB and OF be the height from O to CD. From the similarity, we have:
OEOF=ABCD=2
- Therefore, we can express OE in terms of OF:
OE=2⋅OF(Equation 1)
6. Finding the Area of Triangle COD:
- The area of triangle AOB can be expressed as:
Area of △AOB=12×AB×OE=12×(2x)×OE=x⋅OE
- The area of triangle COD can be expressed as:
Area of △COD=12×CD×OF=12×x×OF
7. Relating the Areas:
- From the similarity of triangles, we know that:
Area of △COD=14⋅Area of △AOB
- Substituting the known area of triangle AOB:
Area of △COD=14×84 cm2=21 cm2
Final Answer:
The area of triangle COD is 21 cm².
---
- We have a trapezium ABCD where AC and BD intersect at point O.
- It is given that AB = 2CD.
- The area of triangle AOB is given as 84 cm².
- Draw trapezium ABCD with AB and CD as the parallel sides.
- Mark the intersection point O where diagonals AC and BD meet.
- Since O is the intersection of diagonals, the angles ∠AOB and ∠COD are vertically opposite angles and are equal.
- The angles ∠OAB and ∠OCD are alternate angles, which are also equal.
- From the above angle relationships, we can conclude that triangles AOB and COD are similar (by AA criterion of similarity).
- Therefore, the ratio of their corresponding sides is equal.
- Let CD = x. Then, AB = 2x (since AB = 2CD).
- The ratio of the sides is:
ABCD=2xx=2
- Let OE be the height from O to AB and OF be the height from O to CD. From the similarity, we have:
OEOF=ABCD=2
- Therefore, we can express OE in terms of OF:
OE=2⋅OF(Equation 1)
- The area of triangle AOB can be expressed as:
Area of △AOB=12×AB×OE=12×(2x)×OE=x⋅OE
- The area of triangle COD can be expressed as:
Area of △COD=12×CD×OF=12×x×OF
- From the similarity of triangles, we know that:
Area of △COD=14⋅Area of △AOB
- Substituting the known area of triangle AOB:
Area of △COD=14×84 cm2=21 cm2
The area of triangle COD is 21 cm².
Topper's Solved these Questions
Similar Questions
The diagonals of a trapezium ABCD with AB||DC intersect each other at point O. If AB = 2CD, find the ratio of the areas of triangle AOB and COD.
View SolutionIn a parallelogram ABCD diagonals AC and BD intersect at O and AC=6.8cm and BD=13.6cm. Find the measures of OC and OD.
View SolutionIn a trapezium PQRS, PQ||SR and PQ= 2 SR. if the diagonals intersect at O and area of △POQ=96cm2 , find the area of △SOR.
View SolutionDiagonals of a trapezium ABCD with AB || DC intersect each other at the point O. If AB = 2 CD, find the ratio of the areas of triangles AOB and COD.
View SolutionLine segments AB and CD intersect at O such that AC∣∣DB . If ∠CAB=350 and ∠CDB=550 find the ∠BOD.
View SolutionIn parallelogram ABCD, P is mid-point of AB. CP and BD intersect each other at point O. If area of ΔPOB=40cm2 and OP:OC= 1:2, find :
(i) Areas of ΔBOC and ΔPBC
(ii) Areas of ΔABC and parallelogram ABCD.
View SolutionABCDEF is a regular hexagon with centre O ). If the area of triangle OAB is 9 cm2 , find the area of: (i) the hexagon and (ii) the circle in which the hexagon is inscribed.
View SolutionIn the adjoining figure, ABCD is a quadrilateral in which AD∣∣BC. AC and BD intersect each other at point 'O'. Prove that:
area of ΔCOD= area of ΔABO
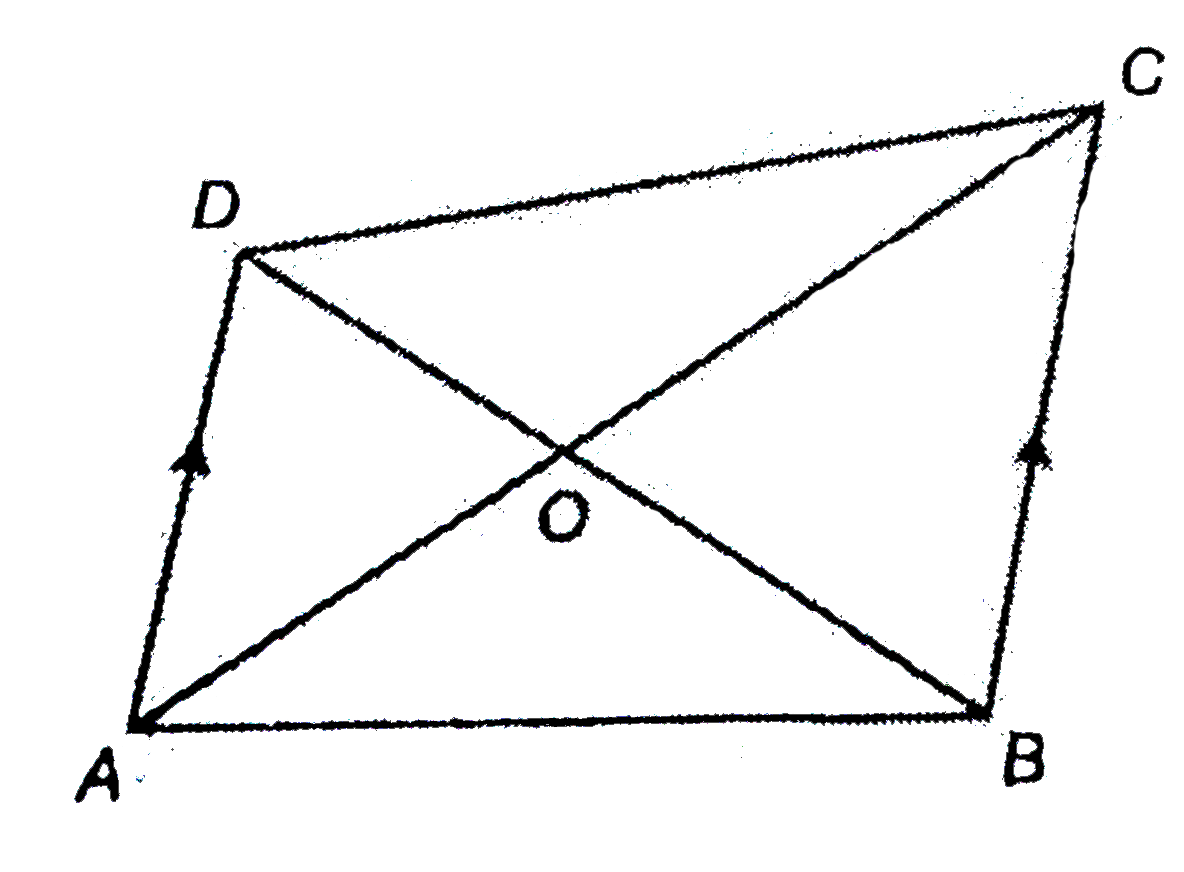
View SolutionABCD is a trapezium in which AB is parallel to CD . The diagonals AC and BD intersect at O . Prove that (i) AOB~COD (ii) If OA=6cm , OC=8cm , Find: Area (AOB)Area (COD) (b) Area (AOD)Area (COD)
View SolutionDiagonal AC and BD of trapezium ABCD, in which AB∣∣DC, intersect each other at O. The triangle which is equal in area of AOD is AOB (b) BOC (c) DOC (d) ADC
View Solution
