A circus artists is climbing a 20m long rope, which is tightly stretched and tied from the top of a vertical pole to the ground. Find the height of the pole if the angle made by the rope with the ground level is 300.
To find the height of the pole using the information provided, we can follow these steps:
Step 1: Understand the problem
We have a vertical pole (let's call it AB) and a rope (AC) that is tied from the top of the pole to a point on the ground (point C). The length of the rope is 20 meters, and it makes an angle of 30 degrees with the ground.
Step 2: Identify the triangle
We can visualize a right triangle formed by the pole (AB), the ground (BC), and the rope (AC). Here, AB is the height of the pole (H), AC is the length of the rope (20 m), and the angle at point C (angle ACB) is 30 degrees.
Step 3: Use the sine function
In a right triangle, the sine of an angle is defined as the ratio of the length of the opposite side (perpendicular) to the length of the hypotenuse. Therefore, we can write:
sin(30∘)=Opposite (Height of the pole, H)Hypotenuse (Length of the rope, 20 m)
Step 4: Substitute values
We know that:
- sin(30∘)=12
- The length of the rope (hypotenuse) is 20 m.
Substituting these values into the equation gives us:
12=H20
Step 5: Solve for H
To find H, we can rearrange the equation:
H=20×12
Calculating this gives:
H=10 m
Conclusion
The height of the pole is 10 meters.
---
We have a vertical pole (let's call it AB) and a rope (AC) that is tied from the top of the pole to a point on the ground (point C). The length of the rope is 20 meters, and it makes an angle of 30 degrees with the ground.
We can visualize a right triangle formed by the pole (AB), the ground (BC), and the rope (AC). Here, AB is the height of the pole (H), AC is the length of the rope (20 m), and the angle at point C (angle ACB) is 30 degrees.
In a right triangle, the sine of an angle is defined as the ratio of the length of the opposite side (perpendicular) to the length of the hypotenuse. Therefore, we can write:
We know that:
- sin(30∘)=12
- The length of the rope (hypotenuse) is 20 m.
To find H, we can rearrange the equation:
The height of the pole is 10 meters.
Topper's Solved these Questions
Similar Questions
A circus artist is climbing a 30 m rope, which is tightly stretched and tied from the top of a vertical pole to the ground. Find the height of the pole to the ground. Find the height of the angle made by the rope with the ground level is 30∘), as shown in the figure.

View SolutionA circus artist is climbing from the ground along a rope stretched from the top of a vertical pole and tied at the ground. The height of the pole is 12 m and the angle made by the rope with ground level is 30∘ . Calculate the distance covered by the artist in climbing to the top of the pole.
View SolutionAn electric pole is 8 m high. A steel wire is tied from its top to A point on the ground at a distance of 8 m from the foot of the pole. What is the length of the wire ?
View SolutionFrom a point on the ground, 20m away from the foot of a vertical tower, the angle of elevation of the top of the tower is 60∘ , what is the length of the tower?
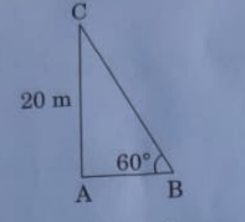
View SolutionIn figure, the angle of elevation of the top of a tower AC from a point B on the ground is 60∘. If the height of the tower is 20m , find the distance of the point from the foot of the tower.
View SolutionIn figure, the angle of elevation of the top of a tower AC from a point B on the ground is 60∘. If the height of the tower is 20m , find the distance of the point from the foot of the tower.
View SolutionWith reference to the given figure, a man stands on the ground at point A, Which is on the same horizontal plane as B, the foot of the vertical pole BC. The height of the pole is 10 m . The man's eye is 2 m above the ground. He observes the angle of elevation of C, the top of the pole, as x∘ , where tan x∘=25 . Calculate :
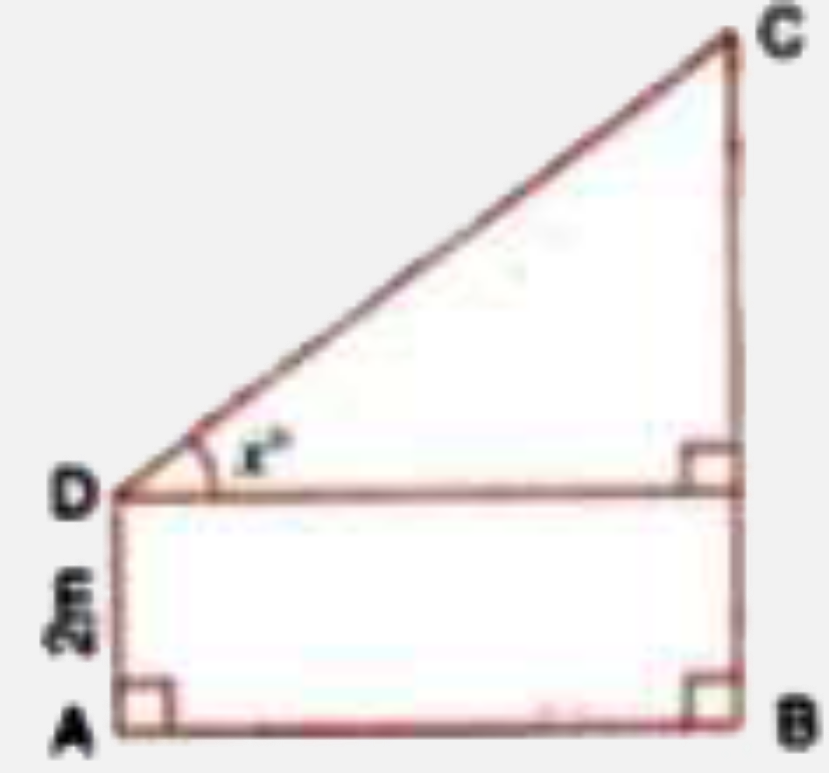
angle of elevation of the top of the pole when he is standing 15 metres from the pole. Give your answer to the nearest degree.
View SolutionThe angle of elevation of the top of a tower from a point on the ground, which is 30m away from the foot of the tower is 30∘ . Find the height of the tower.
View SolutionSome portion of a 20 meters long tree is broken by the wind and its top struck the ground at an angle of 30∘.Find the height of the point where the tree is broken.
View SolutionWith reference to the given figure, a man stands on the ground at point A, Which is on the same horizontal plane as B, the foot of the vertical pole BC. The height of the pole is 10 m . The man's eye is 2 m above the ground. He observes the angle of elevation of C, the top of the pole, as x∘ , where tan x∘=25 . Calculate :

the distance AB in metres ,
View Solution
