The string of a kite is 100 metres long and it makes an angle of 60o with the horizontal. Find the height of the kite, assuming that there is no slack in the string.
To solve the problem of finding the height of the kite, we can follow these steps:
Step 1: Draw the Diagram
Draw a right triangle where:
- Point A is where you are standing.
- Point B is the position of the kite.
- Point C is the point directly below the kite on the horizontal line.
Step 2: Identify the Components
In the triangle:
- The length of the string (hypotenuse AC) is 100 meters.
- The angle between the string and the horizontal (angle CAB) is 60 degrees.
- The height of the kite (perpendicular AB) is what we need to find.
Step 3: Use the Sine Function
We can use the sine function, which relates the angle of a right triangle to the ratio of the opposite side (height of the kite) to the hypotenuse (length of the string):
sin(θ)=oppositehypotenuse
In our case:
sin(60∘)=ABAC
Where:
- AB is the height of the kite (H).
- AC is the length of the string (100 m).
Step 4: Substitute Known Values
Substituting the known values into the sine equation:
sin(60∘)=H100
We know that sin(60∘)=√32, so:
√32=H100
Step 5: Solve for H
To find H, we can rearrange the equation:
H=100×√32
Calculating this gives:
H=50√3
Step 6: Conclusion
Thus, the height of the kite is:
H=50√3 meters
---
Draw a right triangle where:
- Point A is where you are standing.
- Point B is the position of the kite.
- Point C is the point directly below the kite on the horizontal line.
In the triangle:
- The length of the string (hypotenuse AC) is 100 meters.
- The angle between the string and the horizontal (angle CAB) is 60 degrees.
- The height of the kite (perpendicular AB) is what we need to find.
We can use the sine function, which relates the angle of a right triangle to the ratio of the opposite side (height of the kite) to the hypotenuse (length of the string):
sin(θ)=oppositehypotenuse
In our case:
sin(60∘)=ABAC
Where:
- AB is the height of the kite (H).
- AC is the length of the string (100 m).
Substituting the known values into the sine equation:
sin(60∘)=H100
We know that sin(60∘)=√32, so:
√32=H100
To find H, we can rearrange the equation:
H=100×√32
Calculating this gives:
H=50√3
Thus, the height of the kite is:
H=50√3 meters
Topper's Solved these Questions
Similar Questions
The length of a string between a kite and a point on the ground is 90 metres. If the string makes an angle θ with the ground level such that tanθ=158, how high is the kite? Assume that there is no slack in the string.
View SolutionA kite is flying at a height of 60 m above the ground. The string attached to the kite is temporarily tied to a point on the ground. The inclination of the string with the ground is 60∘. Find the length of the string, assuming that there is no slack in the string.
View SolutionA kite is flying at a height of 60m above the ground. The string attached to the kite is temporarily tied to a point on the ground. The inclination of the string with the ground is 60∘ . Find the length of the string assuming that there is no slack in the string.
View SolutionA balloon is connected to a meteorological ground station by a cable of length 215m inclined at 60o to the horizontal. Determine the height of the balloon from the ground. Assume that there is no slack in the cable.
View SolutionTwo masses M and m are connected by a light inextensible string which passes over a small pulley as shown in the diagram. If the mass m is moving downward with a velocity v when the string makes an angle of 45∘ with the horizontal, find the total K.E. of the two masses. AsSigmae that the mass M moves horizontally.
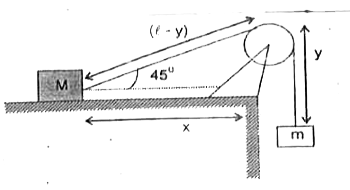
View SolutionA body of mass m is suspended by two strings making angles αandβ with the horizontal. Find the tensions in the strings.
View SolutionA balloon is connected to a meteorological station by a cable of length 200 m inclined to the horizontal at an angle of 60°. Determine the height of the balloon from the ground. Assume that there is no slack in a cable. [Take √3=1.73).
View SolutionThe upper part of a tree broken over by the wind makes an angle of 60∘ with the ground and the horizontal distance from the foot of the tree to the point where the top of the tree meets the ground is 10 metres. Find the height of the tree before broken.
View SolutionA kite is flying at a height of 75 metres from the ground level, attached to a string inclined at 60∘ to the horizontal. Find the length of the string to the nearest metre.
View SolutionA kite is flying at a height of 30m from the ground. The length of string from the kite to the ground is 60m. Assuming that three is no slack in the string, the angle of elevation of the kite at the ground is: 450 (b) 300 (c) 600 (d) 900
View Solution
