A probability distribution of a variable X is given below: X:01234 P(X):0.10.250.30.20.15 Find (i) Var(X) (ii) Var(X2)
To solve the problem, we will follow these steps:
Step 1: Define the random variable and its probability distribution
We are given the random variable X and its corresponding probabilities P(X):
- X:0,1,2,3,4
- P(X):0.1,0.25,0.3,0.2,0.15
Step 2: Calculate E(X) (Expected Value)
The expected value E(X) is calculated using the formula:
E(X)=∑(P(Xi)⋅Xi)
Calculating E(X):
E(X)=(0⋅0.1)+(1⋅0.25)+(2⋅0.3)+(3⋅0.2)+(4⋅0.15)
=0+0.25+0.6+0.6+0.6=2.05
Step 3: Calculate E(X2)
Next, we calculate E(X2):
E(X2)=∑(P(Xi)⋅X2i)
Calculating E(X2):
E(X2)=(02⋅0.1)+(12⋅0.25)+(22⋅0.3)+(32⋅0.2)+(42⋅0.15)
=(0⋅0.1)+(1⋅0.25)+(4⋅0.3)+(9⋅0.2)+(16⋅0.15)
=0+0.25+1.2+1.8+2.4=5.65
Step 4: Calculate Variance V(X)
Variance V(X) is given by the formula:
V(X)=E(X2)−(E(X))2
Substituting the values we calculated:
V(X)=5.65−(2.05)2
Calculating (2.05)2:
(2.05)2=4.2025
Now substituting back:
V(X)=5.65−4.2025=1.4475
Step 5: Calculate Variance V(X/2)
Using the property of variance:
V(aX+b)=a2V(X)
For V(X/2):
V(X/2)=(12)2V(X)=14V(X)
Substituting the value of V(X):
V(X/2)=14⋅1.4475=0.361875
Final Answers
(i) V(X)=1.4475
(ii) V(X/2)=0.361875
---
We are given the random variable X and its corresponding probabilities P(X):
- X:0,1,2,3,4
- P(X):0.1,0.25,0.3,0.2,0.15
The expected value E(X) is calculated using the formula:
E(X)=∑(P(Xi)⋅Xi)
Calculating E(X):
E(X)=(0⋅0.1)+(1⋅0.25)+(2⋅0.3)+(3⋅0.2)+(4⋅0.15)
=0+0.25+0.6+0.6+0.6=2.05
Next, we calculate E(X2):
E(X2)=∑(P(Xi)⋅X2i)
Calculating E(X2):
E(X2)=(02⋅0.1)+(12⋅0.25)+(22⋅0.3)+(32⋅0.2)+(42⋅0.15)
=(0⋅0.1)+(1⋅0.25)+(4⋅0.3)+(9⋅0.2)+(16⋅0.15)
=0+0.25+1.2+1.8+2.4=5.65
Variance V(X) is given by the formula:
V(X)=E(X2)−(E(X))2
Substituting the values we calculated:
V(X)=5.65−(2.05)2
Calculating (2.05)2:
(2.05)2=4.2025
Now substituting back:
V(X)=5.65−4.2025=1.4475
Using the property of variance:
V(aX+b)=a2V(X)
For V(X/2):
V(X/2)=(12)2V(X)=14V(X)
Substituting the value of V(X):
V(X/2)=14⋅1.4475=0.361875
(i) V(X)=1.4475
Topper's Solved these Questions
Similar Questions
The probability distribution of a discreate random variable X is given below :

The value of k is
View SolutionThe probability distribution of a discrate random variable X is given below :
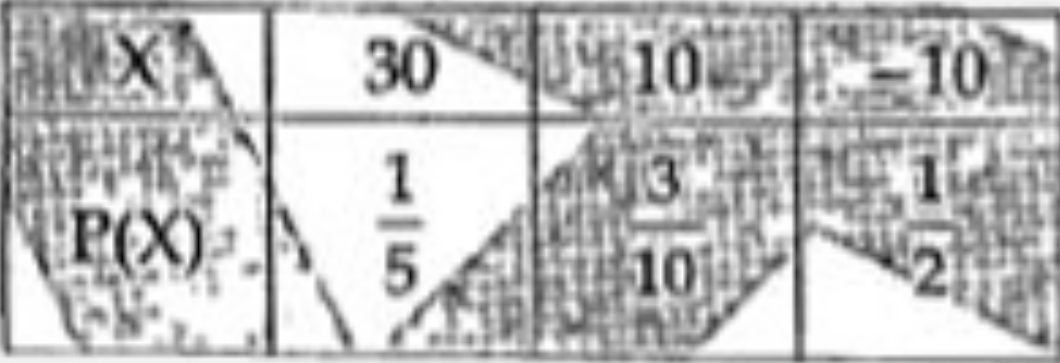
Then E(X) is equal to
View SolutionThe probability distribution of a discrete random variable X is given below

The value of k is
View SolutionConsider the probability distribution of a random variable X.

Variance of X
View SolutionConsider the probability distribution of a random variable X.

V(X2)
View SolutionThe probability distribution function of a random variable X is given by xi:012 pi:3c34c−10c25c−1 Where c>0. Find : (i) c (ii) P(X<2) (iii) P(1<X≤2).
View SolutionThe probability distribution of a random variable X is given below.

Find k, mean and variance of X
View SolutionThe probability distribution of a random variable X is given as under:

Find k , and P (X<6) .
View Solution
is the probability distribution of a random variable X. Find the variance of X.
View Solution
is the probability distribution of a random variable X. Find the variance of X.
View Solution
