A random variable X as the following probability distribution: xi:−2−10123 pi:0.1k0.22k0.3k Find (i) Find the value of k. (ii) Calculate the mean ofX. Calculate the variance of X.
To solve the problem step by step, we will follow the instructions provided in the video transcript.
Step 1: Form the Probability Distribution Table
We have the random variable X with the following values:
xipi−20.1−1k00.212k20.33k
Step 2: Find the Value of k
The sum of all probabilities must equal 1:
0.1+k+0.2+2k+0.3+k=1
Combining like terms:
0.1+0.2+0.3+4k=1
This simplifies to:
0.6+4k=1
Now, isolate k:
4k=1−0.64k=0.4k=0.44=0.1
Step 3: Calculate the Mean of X
The mean E(X) is calculated using the formula:
E(X)=∑(pi⋅xi)
Substituting the values:
E(X)=0.1⋅(−2)+0.1⋅(−1)+0.2⋅0+0.2⋅1+0.3⋅2+0.1⋅3
Calculating each term:
=−0.2−0.1+0+0.2+0.6+0.3
Now, summing these values:
E(X)=−0.2−0.1+0+0.2+0.6+0.3=0.8
Step 4: Calculate the Variance of X
The variance Var(X) is calculated using the formula:
Var(X)=∑(pi⋅x2i)−(E(X))2
First, we calculate ∑(pi⋅x2i):
=0.1⋅(−2)2+0.1⋅(−1)2+0.2⋅02+0.2⋅12+0.3⋅22+0.1⋅32
Calculating each term:
=0.1⋅4+0.1⋅1+0.2⋅0+0.2⋅1+0.3⋅4+0.1⋅9
This simplifies to:
=0.4+0.1+0+0.2+1.2+0.9
Summing these values:
=0.4+0.1+0.2+1.2+0.9=2.8
Now, we can find the variance:
Var(X)=2.8−(0.8)2
Calculating (0.8)2:
=2.8−0.64=2.16
Final Answers
(i) The value of k is 0.1.
(ii) The mean of X is 0.8.
(iii) The variance of X is 2.16.
We have the random variable X with the following values:
The sum of all probabilities must equal 1:
The mean E(X) is calculated using the formula:
The variance Var(X) is calculated using the formula:
(i) The value of k is 0.1.
Topper's Solved these Questions
Similar Questions
A random variable 'X' has the following probability distribution :

The values of k is
View SolutionA random variable X has the following probability distribution:
X: −2 −1 0 1 2 3
P(X):0.1 k 0.2 2k 0.3 k , find value of k
View SolutionA random varibale X has the following probability distribution.
X:12345P(X):00.10.20.30.4
Find the mean.
View SolutionA discrete random variable X has the probability distribution given below: X:0.511.52 P(X):kk22k2k Find the value of k. (ii) Determine the mean of the distribution.
View SolutionA random variable X has the following probability distribution: X=xi: 1 2 3 4 P(X=xi): k 2k 3k 4k Write the value of P(X≥3) .
View SolutionA random variable X has the following probability distribution:
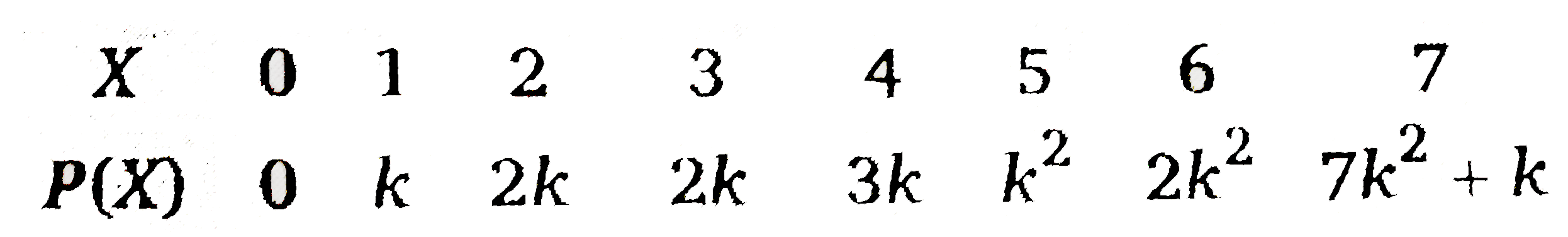
Determine :
(i) k
(ii) P(X<3)
(iii) P(X>6)
(iv) P(0<X<3)
View SolutionA random variable X has the following distribution
X=x1:−2−10123P(X=x1):0.1k0.22k0.3k
The value of k and its mean and variance are
View SolutionFind the mean and standard deviation of the following probability distribution: xi:2 3 4 pi:0.2 0.5 0.3
View SolutionFind the mean and variance for the following probability distribution: ∣∣∣xi1234pi0.40.30.20.1∣∣∣
View SolutionA discrete random variable X has the probability distribution as given below
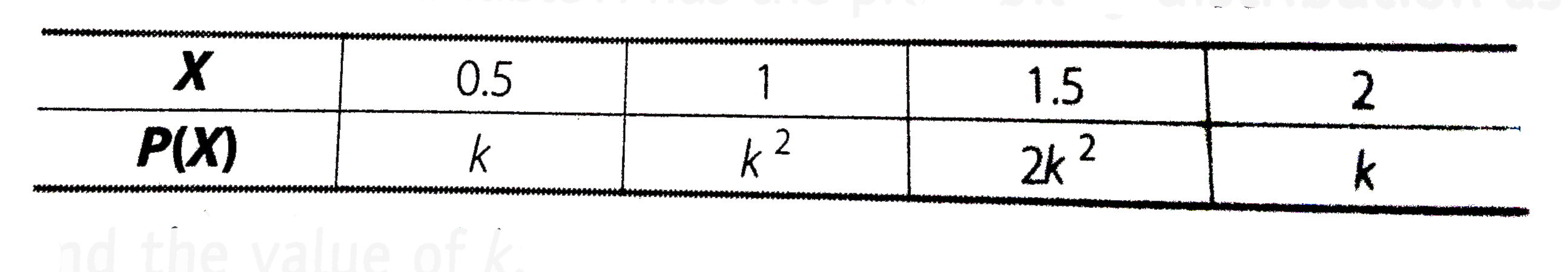
(i) Find the value of k.
(ii) Determine the mean of the distribution.
View Solution
