The probability distribution of a discrete random variable X is given as under: X:1242A3A5A P(X):121/5325110125125 Calculate: The value of A,ifE(X)=2.94 (ii) Variance ofX.
To solve the problem step by step, we will first calculate the value of A given that E(X)=2.94, and then we will calculate the variance of X.
Step 1: Set up the probability distribution table
The random variable X and its corresponding probabilities P(X) are given as follows:
XP(X)11221543252A1103A1255A125
Step 2: Write the equation for E(X)
The expected value E(X) is calculated using the formula:
E(X)=∑P(X)⋅X
Substituting the values, we have:
E(X)=1⋅12+2⋅15+4⋅325+2A⋅110+3A⋅125+5A⋅125
Step 3: Simplify the equation
Calculating each term:
- 1⋅12=12
- 2⋅15=25
- 4⋅325=1225
- 2A⋅110=2A10=A5
- 3A⋅125=3A25
- 5A⋅125=5A25=A5
Now, we can rewrite E(X):
E(X)=12+25+1225+A5+3A25+A5
Step 4: Find a common denominator
The common denominator for 2,5,25 is 50:
- 12=2550
- 25=2050
- 1225=2450
- A5=10A50
- 3A25=6A50
Thus, we have:
E(X)=25+20+24+10A+6A50=69+16A50
Step 5: Set up the equation with the given expected value
We know that E(X)=2.94:
69+16A50=2.94
Step 6: Solve for A
Multiplying both sides by 50:
69+16A=2.94×50
Calculating 2.94×50=147:
69+16A=147
Subtracting 69 from both sides:
16A=147−69
16A=78
Now, dividing by 16:
A=7816=4.875
Step 7: Calculate the variance of X
Variance is calculated using the formula:
Var(X)=E(X2)−(E(X))2
Step 8: Calculate E(X2)
Using the same probabilities, we find E(X2):
E(X2)=12⋅12+22⋅15+42⋅325+(2A)2⋅110+(3A)2⋅125+(5A)2⋅125
Calculating each term:
- 12⋅12=12
- 22⋅15=45
- 42⋅325=4825
- (2A)2⋅110=4A210=2A25
- (3A)2⋅125=9A225
- (5A)2⋅125=25A225=A2
Combining these terms gives:
E(X2)=25+40+48+10A2+9A2+25A250=113+44A250
Step 9: Substitute A and calculate Var(X)
Now substituting A=4.875:
1. Calculate E(X2) using A.
2. Substitute E(X) and E(X2) into the variance formula.
Finally, we can compute the variance.
- 2⋅15=25
- 4⋅325=1225
- 2A⋅110=2A10=A5
- 3A⋅125=3A25
- 5A⋅125=5A25=A5
- 25=2050
- 1225=2450
- A5=10A50
- 3A25=6A50
16A=78
- 22⋅15=45
- 42⋅325=4825
- (2A)2⋅110=4A210=2A25
- (3A)2⋅125=9A225
- (5A)2⋅125=25A225=A2
2. Substitute E(X) and E(X2) into the variance formula.
Topper's Solved these Questions
Similar Questions
The probability distribution of a discrete random variable X is given below
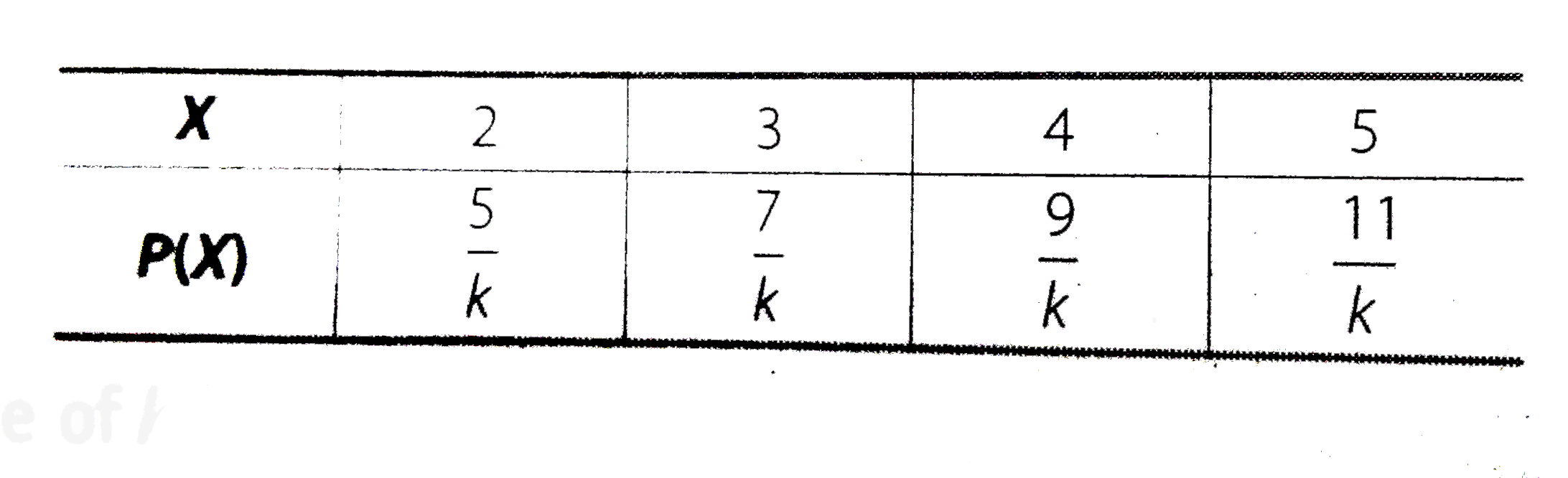
The value of k is
View SolutionThe probability distribution of a discreate random variable X is given below :

The value of k is
View SolutionThe probability distribution of a random variable X is given as under:

Find k , and P (X<6) .
View SolutionConsider the probability distribution of a random variable X.

Variance of X
View Solution
is the probability distribution of a random variable X. Find the variance of X.
View Solution
is the probability distribution of a random variable X. Find the variance of X.
View SolutionConsider the probability distribution of a random variable X.

V(X2)
View SolutionThe probability distribution of a random variable X is given below.

Find k, mean and variance of X
View SolutionThe probability distribution of a discrete random variable X is given below: X: 2 3 4 5 P(X):5k 7k 9k 11k The value of E(X) is
View SolutionThe probability distribution for a random variable X is as follows:
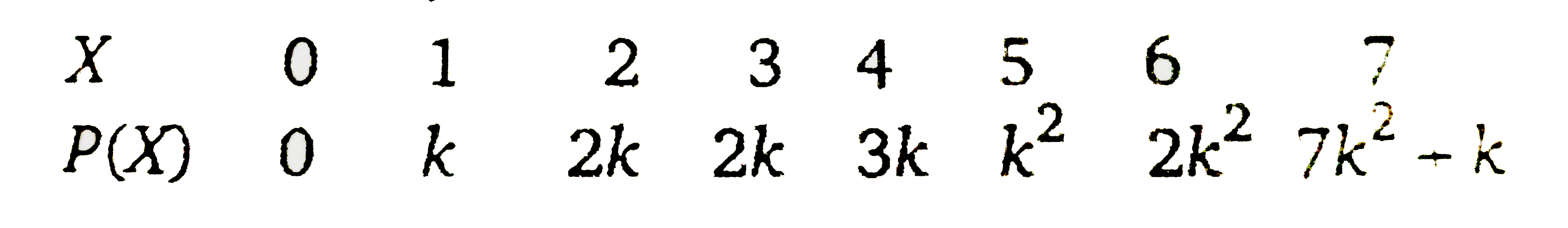
Find:
(i) k (ii) P(X<3) (iii) P(X>6)(iv)P(0X<3)
View Solution
