The probability distribution of a discrete random variable X is given below:
X: 2 3 4 5
P(X):5k 7k 9k 11k
The value of E(X) is
To find the expected value E(X) of the discrete random variable X with the given probability distribution, we will follow these steps:
Step 1: Set up the equation for the sum of probabilities
We know that the sum of all probabilities must equal 1. Given the probabilities:
P(X)=5k,7k,9k,11k
We can write the equation:
5k+7k+9k+11k=1
Step 2: Combine the fractions
Combining the fractions gives us:
5+7+9+11k=1
Calculating the sum in the numerator:
5+7+9+11=32
So we have:
32k=1
Step 3: Solve for k
Now, we can solve for k:
k=32
Step 4: Calculate the expected value E(X)
The expected value E(X) is calculated using the formula:
E(X)=∑(x⋅P(X))
Substituting the values of X and P(X):
E(X)=2⋅5k+3⋅7k+4⋅9k+5⋅11k
Substituting k=32:
E(X)=2⋅532+3⋅732+4⋅932+5⋅1132
Step 5: Simplify the expression
Calculating each term:
E(X)=1032+2132+3632+5532
Combining these fractions:
E(X)=10+21+36+5532=12232
Step 6: Final calculation
Now, we can simplify 12232:
E(X)=3.8125
Thus, the expected value E(X) is:
3.8125
We know that the sum of all probabilities must equal 1. Given the probabilities:
Combining the fractions gives us:
Now, we can solve for k:
The expected value E(X) is calculated using the formula:
Calculating each term:
Now, we can simplify 12232:
Topper's Solved these Questions
Similar Questions
The probability distribution of a discrete random variable X is given below
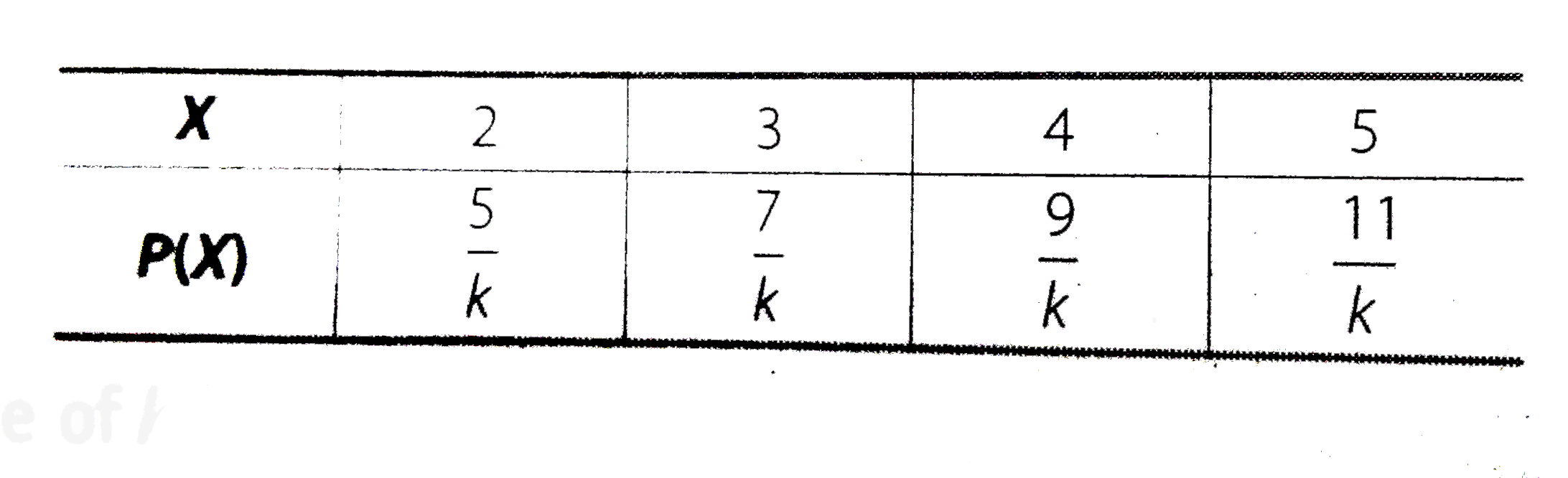
The value of k is
View SolutionThe probability distribution of a discreate random variable X is given below :

The value of k is
View SolutionThe probability distribution of a discrate random variable X is given below :
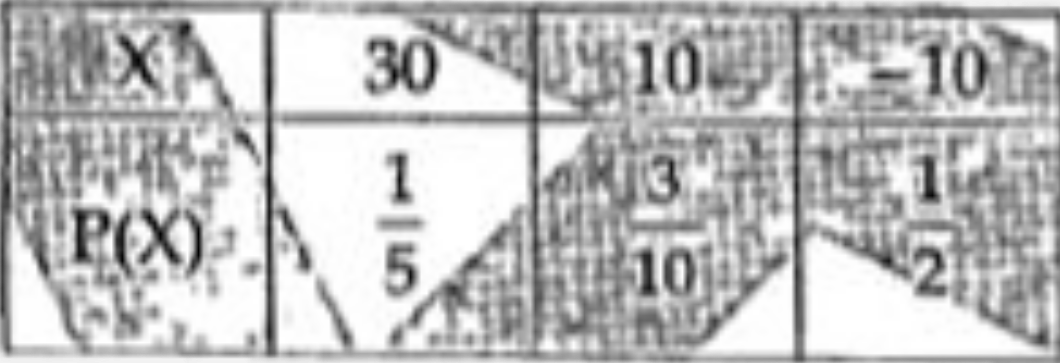
Then E(X) is equal to
View SolutionIf the probability distribution of a random variable X is given by X=xi: 1 2 3 4 P(X=xi): 2k 4k 3k k Write the value of k .
View SolutionThe probability distribution of a random variable X is given below.

Find k, mean and variance of X
View SolutionFind the value of k for probability distribution of a random variable X is give by:

View SolutionThe probability distribution of a random variable X is given as under:

Find k , and P (X<6) .
View SolutionThe probability distribution of a random variable X is given below: X: 0 1 2 3 P(X):k k2 k4 k8 (i) Determine the value of k (ii) Determine P(X≤2)and P(X>2) (iii) Find P(X≤2)+P(X>2)
View SolutionThe probability of a random variable X is given below
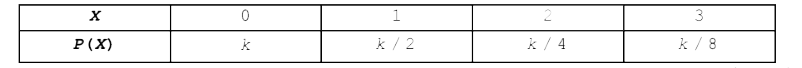
Determine the value of k
View SolutionThe following is the probability distribution of a random vaiable X.
The value of k is
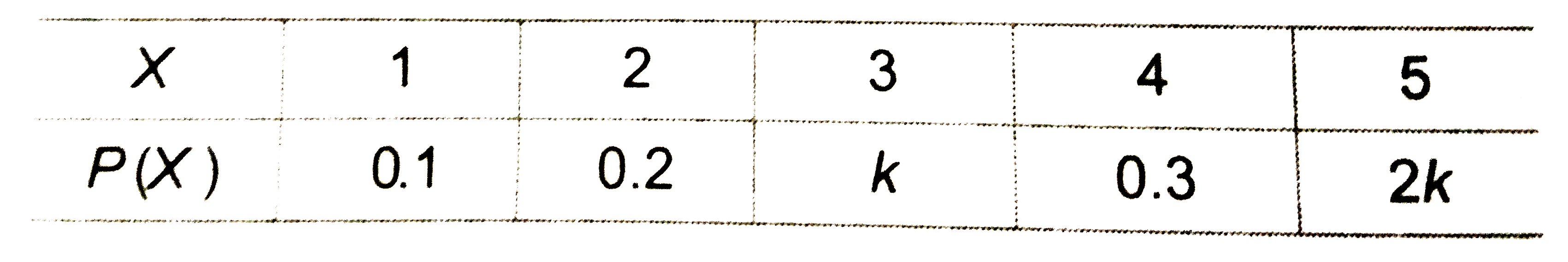
View Solution
