Define value of a polynomial at a point.
To define the value of a polynomial at a point, we can follow these steps:
Step 1: Understanding the Definition
A polynomial is a mathematical expression that can be written in the form of p(x)=anxn+an−1xn−1+…+a1x+a0, where an,an−1,…,a0 are constants (coefficients) and n is a non-negative integer (degree of the polynomial).
Step 2: Define the Value of a Polynomial at a Point
The value of a polynomial at a specific point x=c is obtained by substituting c into the polynomial function. This means we replace every instance of x in the polynomial with the value c.
Step 3: Example of Finding the Value
Let's take an example polynomial:
p(x)=x+1
To find the value of this polynomial at the point x=1:
1. Substitute x with 1:
p(1)=1+1
2. Calculate the result:
p(1)=2
Conclusion
Thus, the value of the polynomial p(x) at the point x=1 is 2.
Summary
In summary, the value of a polynomial at a point is determined by substituting the point into the polynomial and calculating the result.
---
A polynomial is a mathematical expression that can be written in the form of p(x)=anxn+an−1xn−1+…+a1x+a0, where an,an−1,…,a0 are constants (coefficients) and n is a non-negative integer (degree of the polynomial).
The value of a polynomial at a specific point x=c is obtained by substituting c into the polynomial function. This means we replace every instance of x in the polynomial with the value c.
Let's take an example polynomial:
p(x)=x+1
1. Substitute x with 1:
p(1)=1+1
2. Calculate the result:
p(1)=2
Thus, the value of the polynomial p(x) at the point x=1 is 2.
In summary, the value of a polynomial at a point is determined by substituting the point into the polynomial and calculating the result.
Topper's Solved these Questions
Similar Questions
Knowledge Check
x−5−3−11y04−30
Four points on the graph of a polynomial P are shown in the table above. If P is a polynomial of degree 3, then P(x) could equal
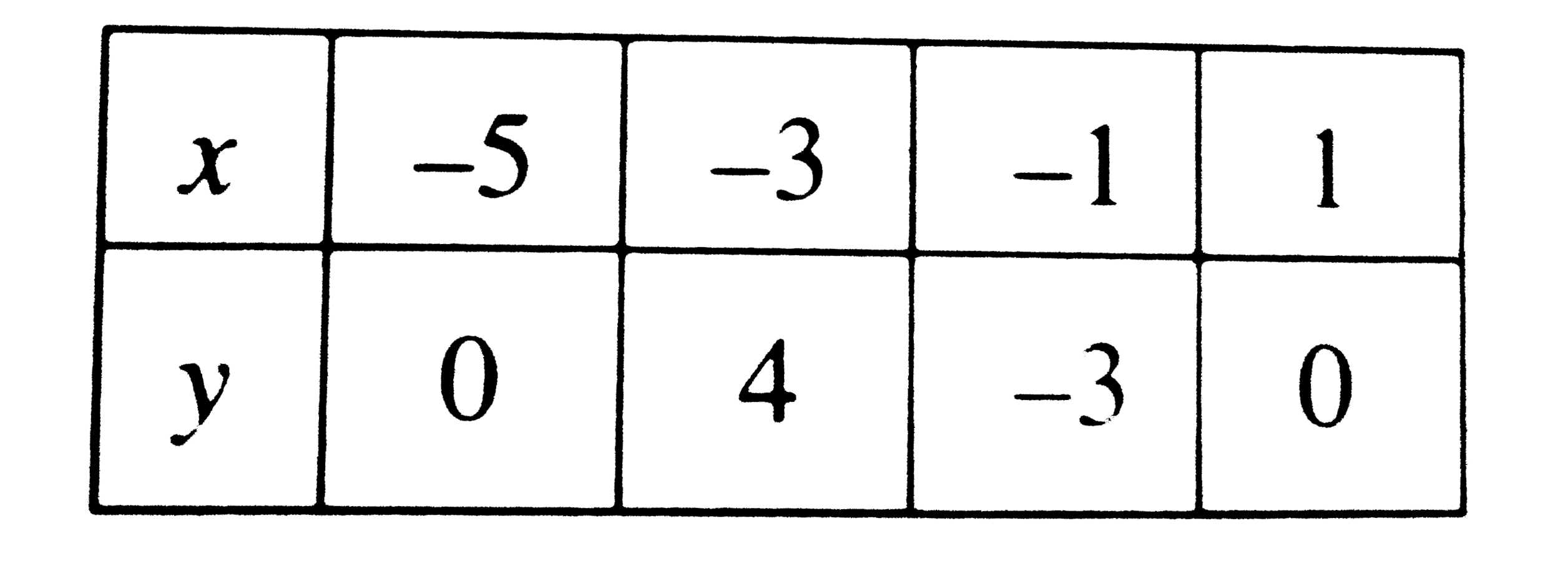 Aa(x-5)(x-2)(x+1)Ba(x-5)(x+2)(x+1)Ca(x+5)(x-2)(x-1)Da(x+5)(x+2)(x-1)
Aa(x-5)(x-2)(x+1)Ba(x-5)(x+2)(x+1)Ca(x+5)(x-2)(x-1)Da(x+5)(x+2)(x-1)The value of the polynomial 3x2+5x−2 at x = - 3 is
A38B24C12D8For x = 0, the value of the polynomial x3+9x+5 is:
A9B0C−9D5
A polynomial in x of degree 3 vanishes when x=1 and x=−2 , ad has the values 4 and 28 when x=−1 and x=2 , respectively. Then find the value of polynomial when x=0 .
View SolutionDefine a polynomial with real coefficients.
View SolutionDefine continuity of a function at a point.
View SolutionDefine differentiability of a function at a point.
View SolutionThe possible values of x for which the value of the polynomial f(x)=3x3+2x2−19x+6 is zero are
View Solution