If graph of quadratic polynomial ax2+bx+c cuts positive direction of y-axis, then what is the sign of c ?
To determine the sign of c in the quadratic polynomial ax2+bx+c given that its graph cuts the positive direction of the y-axis, we can follow these steps:
1. Understanding the Polynomial: The quadratic polynomial is given as ax2+bx+c.
2. Identifying the Y-Intercept: The graph of the polynomial intersects the y-axis when x=0. To find this point, we substitute x=0 into the polynomial.
y=a(0)2+b(0)+c=c
3. Interpreting the Y-Intercept: The value of y when x=0 is equal to c. Therefore, the point where the graph cuts the y-axis is (0,c).
4. Analyzing the Given Condition: The problem states that the graph cuts the positive direction of the y-axis. This means that the y-coordinate of the point where the graph intersects the y-axis must be positive.
5. Conclusion About c: Since the graph cuts the positive direction of the y-axis, it implies that c>0.
Thus, we conclude that the sign of c is positive.
Final Answer:
The sign of c is positive.
---
y=a(0)2+b(0)+c=c
The sign of c is positive.
Topper's Solved these Questions
Similar Questions
Knowledge Check
If a, b, c are the angles that a line makes with the positive directions of x, y and z axis, respectively, then the direction cosines of the lines are
Asin a, sin b, sin cBcos a, cos b, cos cCtan a, tan b, tan cDnone of the above
If graph of the quadratic y=ax2+bx+c is given below :
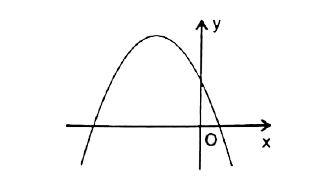 then:
then:
View SolutionThe graph of a quadratic polynomial y=ax2+bx+c,a,b,εR is shown. Find its vertex,roots and D.
View SolutionThe graph of the quadratic trinomial u=ax2+bx+c has its vertex at (4, -5) and two x-intercepts, one positive and one negative. Which of the following holds good? a. a>0 b. b<0 c. c<0 d. 8a=b
View SolutionIf a line makes an angle of π4 with the positive direction of each of x-axis and y-axis, then the angel that the line makes with the positive direction of the z-axis is a. π3 b. π4 c. π2 d. π6
View SolutionIf a line makes an angle of π4 with the positive direction of each of x-axis and y-axis, then the angle that the line makes with the positive direction of the z-axis is a. π3 b. π4 c. π2 d. π6
View SolutionIf a,b,c ∈R, then for which of the following graphs of the quadratic polynomial y=ax2−2bx+c(a≠0), the product (abc) is negative ?
View SolutionA quadratic polynomial maps from [-2,3] onto [0,3] and touches X-axis at x=3, then the polynomial is
View Solution
