In Fig. 4.31, if and , prove that is isosceles. (FIGURE)
To prove that triangle CAB is isosceles given the conditions ADDC=BEEC and ∠CDE=∠CED, we can follow these steps:
1. Given Information:
We have ADDC=BEEC and ∠CDE=∠CED.
2. Apply the Converse of the Basic Proportionality Theorem:
According to the Basic Proportionality Theorem (also known as Thales' theorem), if a line divides two sides of a triangle in the same ratio, then it is parallel to the third side. Here, since ADDC=BEEC, we can conclude that line DE is parallel to line AB.
Hint: Remember that if two segments are proportional, the line connecting them is parallel to the third side.
3. Corresponding Angles:
Since DE is parallel to AB, the angles formed are corresponding angles. Therefore, we have:
∠CDE=∠CAB(1)
and
∠CED=∠CBA(2)
4. Use the Given Angles:
From the problem, we know that ∠CDE=∠CED. This means:
∠CAB=∠CBA(from (1) and (2))
5. Conclusion:
Since ∠CAB=∠CBA, by the property of triangles, the sides opposite to equal angles are equal. Therefore, we conclude that:
AC=BC
This means triangle CAB is isosceles.
Final Statement:
Thus, we have proved that triangle CAB is isosceles.
---
We have ADDC=BEEC and ∠CDE=∠CED.
According to the Basic Proportionality Theorem (also known as Thales' theorem), if a line divides two sides of a triangle in the same ratio, then it is parallel to the third side. Here, since ADDC=BEEC, we can conclude that line DE is parallel to line AB.
Since DE is parallel to AB, the angles formed are corresponding angles. Therefore, we have:
∠CDE=∠CAB(1)
and
∠CED=∠CBA(2)
From the problem, we know that ∠CDE=∠CED. This means:
∠CAB=∠CBA(from (1) and (2))
Since ∠CAB=∠CBA, by the property of triangles, the sides opposite to equal angles are equal. Therefore, we conclude that:
AC=BC
This means triangle CAB is isosceles.
Thus, we have proved that triangle CAB is isosceles.
Topper's Solved these Questions
Similar Questions
In Fig. 4.145, if AB⊥BC , DC⊥BC and DE⊥AC , prove that CED∼ABC . (FIGURE)
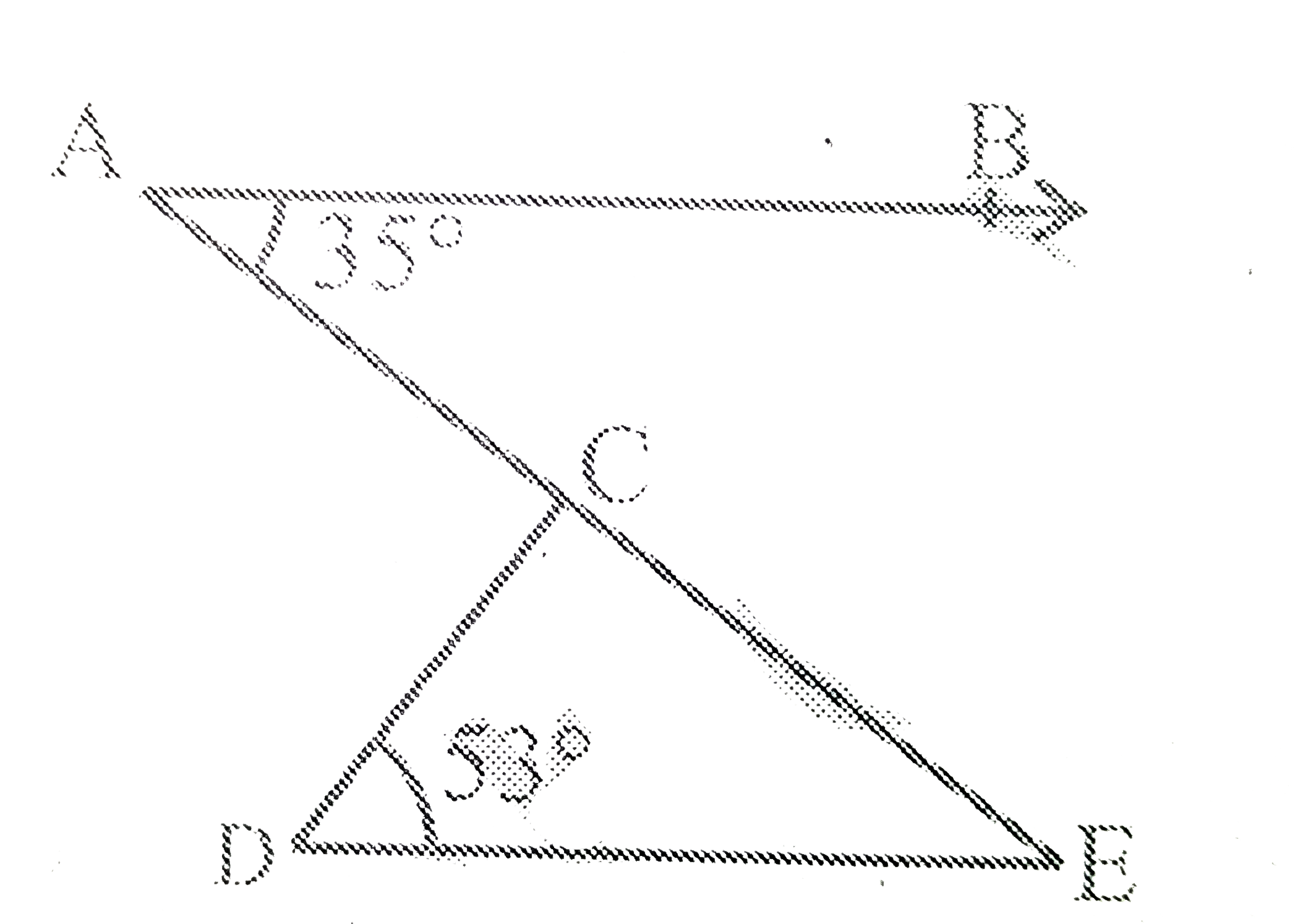
View SolutionIn Fig. 6.41, if AB∣∣DE,∠BAC=35∘ and ∠CDE=53∘, find ∠DCE.
View SolutionIn Fig. 4.143, ∠A=∠CED , prove that CAB∼CED . Also, find the value of x . (FIGURE)
View SolutionIn Figure, if AB∣∣DE,∠BAC=350 and ∠CDE=530 , find ∠DCE.
View SolutionIn Fig. 4.125, FEC≅GBD and ∠1=∠2 . Prove that ADEABC . (FIGURE)
View SolutionIn Figure, AC=AE, AB=AD and ∠BAD=∠EAC. Prove that BC=DE
View SolutionIf D and E are points on sides AB and AC respectively of a triangle ABC such that DE∣∣BC and BD=CE . Prove that ABC is isosceles.
View SolutionIn Figure, BD and CE are two altitudes of a ABC such that BD=CE. Prove that ABC is isosceles. Figure
View SolutionIn Figure, it is given that AB=CF, EF=BD and ∠AFE= ∠CBD. Prove that AFE ≅CBD
View SolutionIn Figure, if AB=AC and BE=CD, prove that AD=AE.
View Solution
