Question

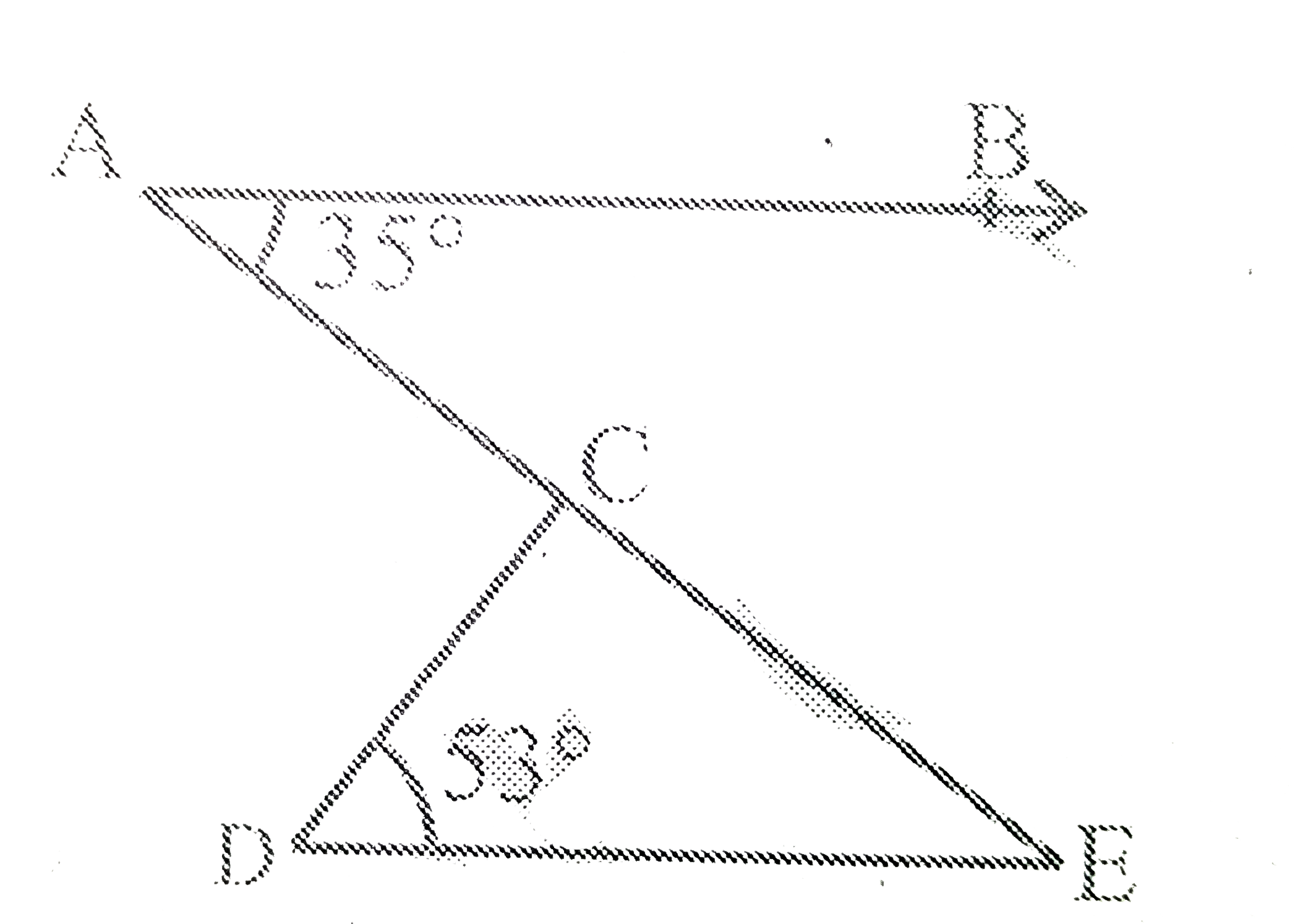
In Figure, if $AB\mid \mid DE,\angle BAC={35}^0$
and $\angle CDE={53}^0$
, find $\angle DCE$.

Explanation

To solve the problem step by step, we will use the properties of parallel lines and triangles.

Step 1: Identify the Given Information
We are given:
- \( AB \parallel DE \)
- \( \angle BAC = 35^\circ \)
- \( \angle CDE = 53^\circ \)

Step 2: Use the Property of Alternate Angles
Since \( AB \parallel DE \), we can use the property of alternate angles. According to this property, alternate angles are equal when a transversal crosses two parallel lines.

Thus, we have:
\( \angle BAC = \angle DEC \)
Therefore,
\( \angle DEC = 35^\circ \)

Step 3: Analyze Triangle DCE
Now, we will consider triangle \( DCE \). The sum of the angles in any triangle is \( 180^\circ \). Therefore, we can write:
\( \angle DCE + \angle CDE + \angle DEC = 180^\circ \)

Step 4: Substitute Known Values
We know:
- \( \angle CDE = 53^\circ \)
- \( \angle DEC = 35^\circ \)

Substituting these values into the equation gives:
\( \angle DCE + 53^\circ + 35^\circ = 180^\circ \)

Step 5: Simplify the Equation
Now, we can simplify the equation:
\( \angle DCE + 88^\circ = 180^\circ \)

Step 6: Solve for Angle DCE
To find \( \angle DCE \), we subtract \( 88^\circ \) from \( 180^\circ \):
\( \angle DCE = 180^\circ - 88^\circ = 92^\circ \)

Conclusion
Thus, the measure of \( \angle DCE \) is:
\( \angle DCE = 92^\circ \)

---