In Figure, CD and GH are respectively the medians of ABC and EFG . If ABC~FEG , prove that (i)ADC~FHG (ii)CDGH=ABFE (iii)CDB~GHE
Step by step video & image solution for In Figure, C D and G H are respectively the medians of A B C and E F G . If A B C ~ F E G , prove that (i) A D C ~ F H G (ii) (C D)/(G H)=(A B)/(F E) (iii) C D B ~ G H E by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
In Fig. 4.102 (i) and (ii) , if CD and GH (D and H lie on AB and FE ) are respectively bisectors of ∠ACB and ∠EGF and ABC~FEG , prove that (FIGURE) DCA~HGF (ii) CDGH=ACFG (iii) DCB~HGE
View SolutionIn Figure, AB=AC.BE and CF are respectively the bisectors of ∠B and ∠C . Prove that ECB ≅ FCB
View SolutionIn Figure, AD and BE are medians of ABC and BE∣∣DF . Prove that CF=14AC.
View SolutionIn Figure, AD, and BE are medians of ABC and BE∣∣DF. Prove that CF=14AC.
View SolutionCD and GH are respectively the bisectors of ∠ACB and ∠EGF such that D and H lie on sides AB and FE of ΔABCandΔEFG respectively. If ΔABC~ΔFEG, show that:
(i) CDGH=AGFG
(ii) ΔDCB~ΔHGE
(iii) ΔDCA~ΔHGF
View SolutionIf E,F,G and H are respectively the mid-points of the sides of a parallelogram ABCD, show that ar(EFGH)=12ar(ABCD)
View SolutionIn Fig. 4.101, AD and CE are two altitudes of ABC . Prove that AEF~CDF (ii) ABD~CBE
View SolutionIf E,F,G and H are respectively the mid-points of the sides of a parallelogram ABCD, show that ar(EFGH)=12ar(ABCD).
View Solution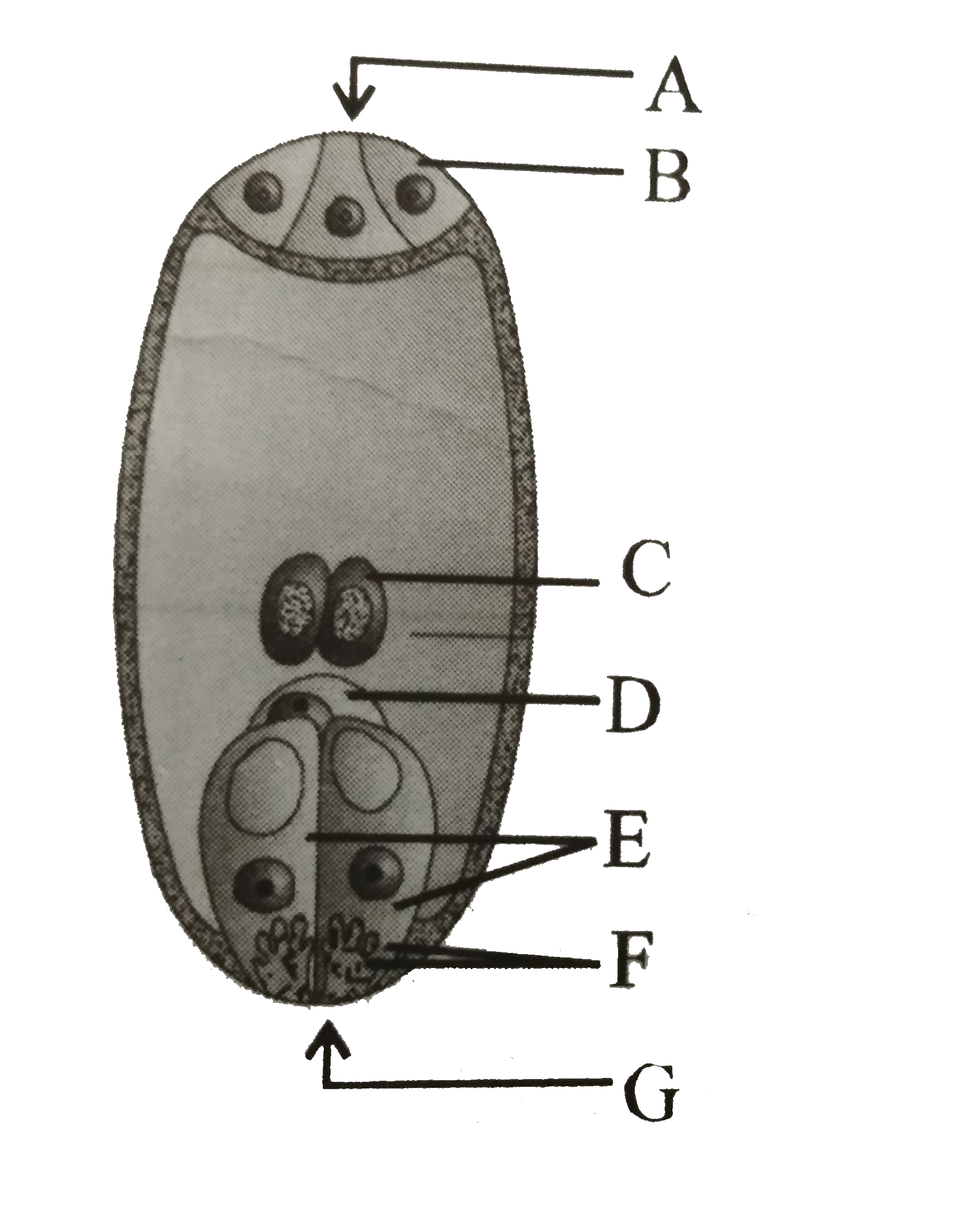
Identify A, B, C, D, E, F,G
View SolutionIn Figure, DEFG is a square and ∠BAC=90 . Prove that (i) A G F ~ D B G(ii)AGF~EFC (iii) D B G ~ E F C(iv)DE2=BDxEC
View Solution
