A right triangle has hypotenuse of length p cm and one side of length q cm . If p−q=1 , find the length of the third side of the triangle.
To solve the problem step by step, we will use the Pythagorean theorem, which states that in a right triangle, the square of the length of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the lengths of the other two sides.
1. Identify the Given Information:
- Let the length of the hypotenuse be p cm.
- Let one side be q cm.
- We know that p−q=1.
2. Express p in terms of q:
- From the equation p−q=1, we can express p as:
p=q+1
3. Set Up the Pythagorean Theorem:
- According to the Pythagorean theorem:
p2=q2+x2
- Here, x is the length of the third side we want to find.
4. Substitute p into the Equation:
- Substitute p=q+1 into the Pythagorean theorem:
(q+1)2=q2+x2
5. Expand the Left Side:
- Expanding (q+1)2:
q2+2q+1=q2+x2
6. Simplify the Equation:
- Subtract q2 from both sides:
2q+1=x2
7. Solve for x:
- Rearranging gives us:
x2=2q+1
- Taking the square root of both sides gives:
x=√2q+1
8. Final Answer:
- Therefore, the length of the third side is:
x=√2q+1 cm
- Let the length of the hypotenuse be p cm.
- Let one side be q cm.
- We know that p−q=1.
- From the equation p−q=1, we can express p as:
p=q+1
- According to the Pythagorean theorem:
p2=q2+x2
- Here, x is the length of the third side we want to find.
- Substitute p=q+1 into the Pythagorean theorem:
(q+1)2=q2+x2
- Expanding (q+1)2:
q2+2q+1=q2+x2
- Subtract q2 from both sides:
2q+1=x2
- Rearranging gives us:
x2=2q+1
- Taking the square root of both sides gives:
x=√2q+1
- Therefore, the length of the third side is:
x=√2q+1 cm
Topper's Solved these Questions
Similar Questions
Knowledge Check
If length of hypotenuse of a right-angled triangle exceeds the length of one side by 2cm and exceeds twice the length of other side by 1cm, then the length of hypotenuse of the triangle is:
A17cmB1cmC15cmD22cm
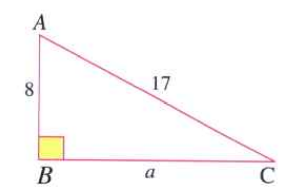
Find the length of side BC in the given triangle.
View SolutionIf two sides of a tringle are of length 5 cm and 1.5 cm, then the length of third side of the triangle cannot be
View SolutionIn a right-angled triangle, the square of the longest side is 625 sq. cm. if the length of the second side is 7 cm, find the length of the third side of the triangle.
View SolutionDraw a right triangle having hypotenuse of length 5.4 cm, and one of the acute angles of measure300.
View SolutionDraw a right triangle having hypotenuse of length 5.4 cm, and one of the acute angles of measure 600.
View SolutionThe perimeter of a triangle is 30cm. Two sides are 12cm and 10cm. What is the length of the third side of the triangle?
View SolutionThe hypotenuse of a right triangle is 13cm long. If one of the remaining two sides is of length 5cm, find the length of another side.
View Solution