In a , right angled at , if , find the value of .
To solve the problem step by step, we will follow the instructions given in the video transcript and apply trigonometric identities.
Step 1: Understand the Triangle Configuration
We have a right-angled triangle ABC with the right angle at A. The angles are defined as follows:
- Angle A = 90°
- Angle B = ∠B
- Angle C = ∠C
Step 2: Use the Given Information
We are given that tanC=√3. By the definition of tangent:
tanC=OppositeAdjacent=ABAC
This means:
ABAC=√3
Let AC=1 (the adjacent side), then:
AB=√3⋅AC=√3⋅1=√3
Step 3: Find the Length of BC
Using the Pythagorean theorem:
BC2=AB2+AC2
Substituting the values we have:
BC2=(√3)2+(1)2=3+1=4
Thus:
BC=√4=2
Step 4: Calculate sinB, cosB, sinC, and cosC
Now we can find the sine and cosine values for angles B and C:
- For angle B:
sinB=ACBC=12
cosB=ABBC=√32
- For angle C:
sinC=ABBC=√32
cosC=ACBC=12
Step 5: Calculate sinBcosC+cosBsinC
Now we can substitute these values into the expression:
sinBcosC+cosBsinC=(12⋅12)+(√32⋅√32)
Calculating each term:
=14+34=1+34=44=1
Final Answer
Thus, the value of sinBcosC+cosBsinC is:
1
We have a right-angled triangle ABC with the right angle at A. The angles are defined as follows:
- Angle A = 90°
- Angle B = ∠B
- Angle C = ∠C
We are given that tanC=√3. By the definition of tangent:
tanC=OppositeAdjacent=ABAC
This means:
ABAC=√3
Let AC=1 (the adjacent side), then:
AB=√3⋅AC=√3⋅1=√3
Using the Pythagorean theorem:
BC2=AB2+AC2
Substituting the values we have:
BC2=(√3)2+(1)2=3+1=4
Thus:
BC=√4=2
Now we can find the sine and cosine values for angles B and C:
- For angle B:
sinB=ACBC=12
cosB=ABBC=√32
sinC=ABBC=√32
cosC=ACBC=12
Now we can substitute these values into the expression:
sinBcosC+cosBsinC=(12⋅12)+(√32⋅√32)
Calculating each term:
=14+34=1+34=44=1
Thus, the value of sinBcosC+cosBsinC is:
1
Topper's Solved these Questions
Similar Questions
In △ABC , right angled at B , if tanA=1√3 , find the value of (i) sinAcosC+cosAsinC (ii) cosAcosC−sinAsinC
View SolutionIn a ΔABC right angled at C, if tanA=1√3 , find the value of sinAcosB+cosAsinB.
View SolutionIn triangle ABC, right-angled at B. if tanA=1√3find the value of:
(i) sinAcosC+cosAsinC
(ii) cosAcosCsinAsinC
View SolutionIn a △ABC right angled at B , ∠A=∠C . Find the values of (i) sinAcosC+cosAsinC (ii) sinAsinB+cosAcosB
View SolutionFrom the following figure, find the values of :
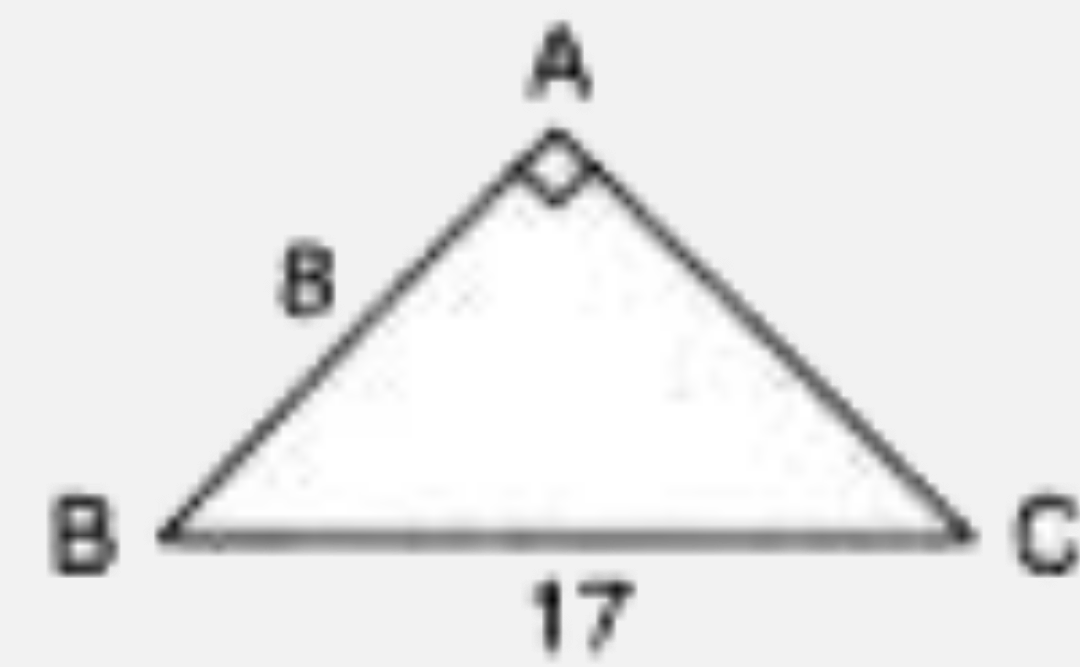 sinB.cosC+cosB.sinC
sinB.cosC+cosB.sinC
View SolutionIn a △ABC , right angled at B , if AB=12 and BC=5 , find: (i) sinA and tanA (ii) cosC and cotC
View SolutionIn a △ABC , right angled at B , if AB=4 and BC=3 , find all the six trigonometric ratios of ∠A .
View SolutionIn ΔABC , ∠A is right - angled . If AB= 1 cm , AC =3 cm and BC = √10 cm , then find the values of cos B and sin C.
View SolutionIn Figure, ABC is right angled at B ,BC=7cm and AC−AB=1cm . Find the value of cosA−sinA.
View SolutionIn a right triangle ABC, right angled at C, if a = 7 cm and b = 7√3 cm, then ∠A=
View Solution
