In Figure, QR is a common tangent to the given circles touching externally at the point T . The tangent at T meets QR at P . If PT=3.8cm , then the length of QR (in cm) is (a) 3.8 (b) 7.6 (c) 5.7 (d) 1.9
To solve the problem step by step, we will follow the reasoning provided in the video transcript.
1. Understanding the Configuration: We have two circles that touch each other externally at point T. The line segment QR is a common tangent to both circles, and it touches the circles at point T. The tangent at point T meets QR at point P.
2. Given Information: We know that PT = 3.8 cm.
3. Using the Tangent Properties: According to the properties of tangents drawn from an external point to a circle, the lengths of the tangents from point P to the points of tangency on each circle are equal. Therefore:
- Let QP be the tangent from point P to the left circle.
- Let PR be the tangent from point P to the right circle.
From the property of tangents, we have:
- QP = PT
- PR = PT
Since PT = 3.8 cm, we can conclude:
- QP = 3.8 cm
- PR = 3.8 cm
4. Finding the Length of QR: The total length of the common tangent QR can be calculated by adding the lengths of QP and PR:
QR=QP+PR=3.8cm+3.8cm=7.6cm
5. Conclusion: Therefore, the length of QR is 7.6 cm.
Final Answer:
The length of QR is 7.6 cm (Option b).
- Let QP be the tangent from point P to the left circle.
- Let PR be the tangent from point P to the right circle.
- QP = PT
- PR = PT
- QP = 3.8 cm
- PR = 3.8 cm
QR=QP+PR=3.8cm+3.8cm=7.6cm
The length of QR is 7.6 cm (Option b).
Topper's Solved these Questions
Similar Questions
In the given figure, PA and PB are tangents to the circle from an external point P. CD is another tangent touching the circle at Q. If PA =12 cm, QC=3cm, then find PC+PD.
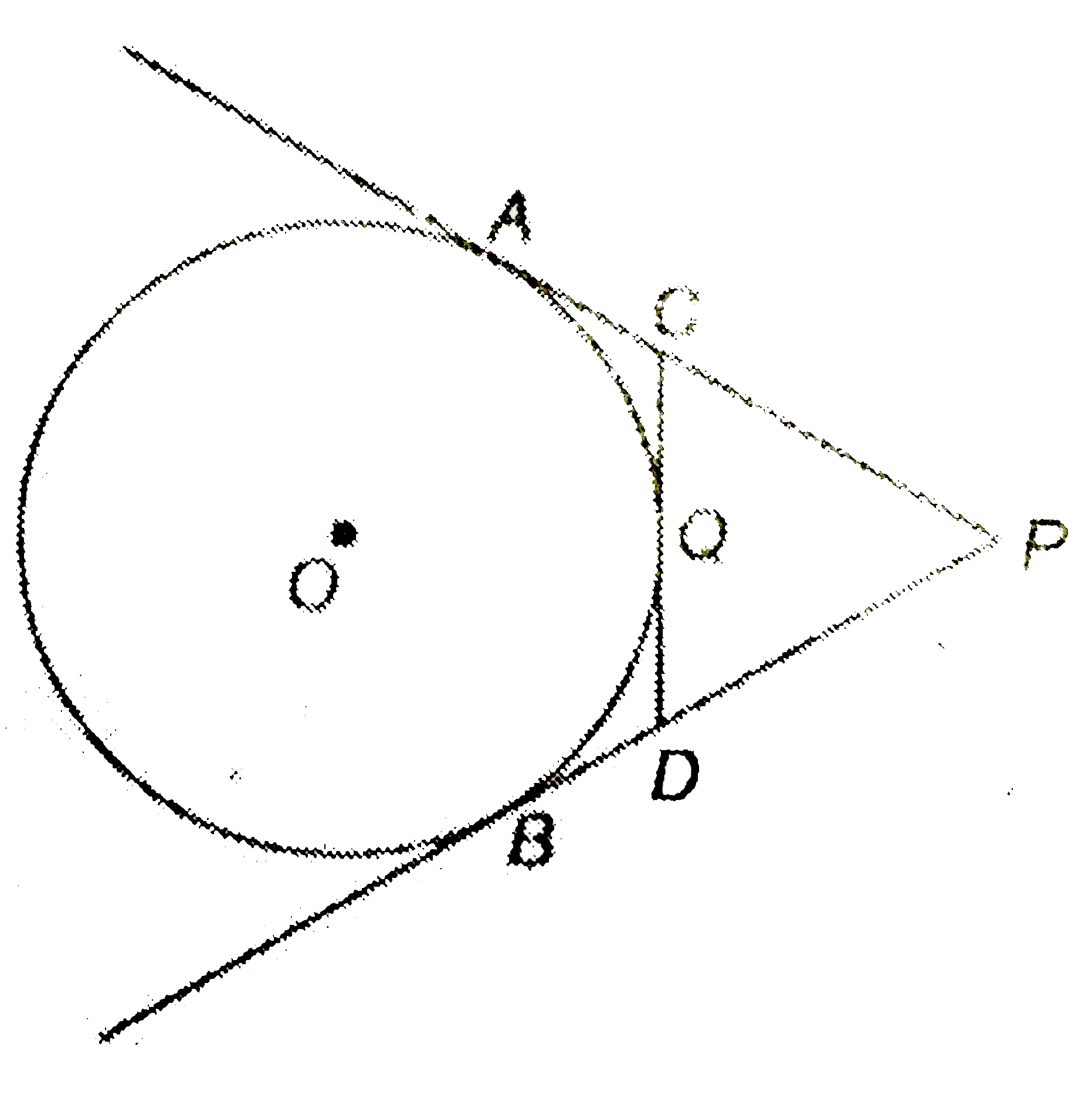
View SolutionIn the given figure PA and PB are tangents to the circle drawn from an external point P. CD is a third tangent touching the circle at Q. If PB=10cm and CQ=2cm. What is the length of PC?
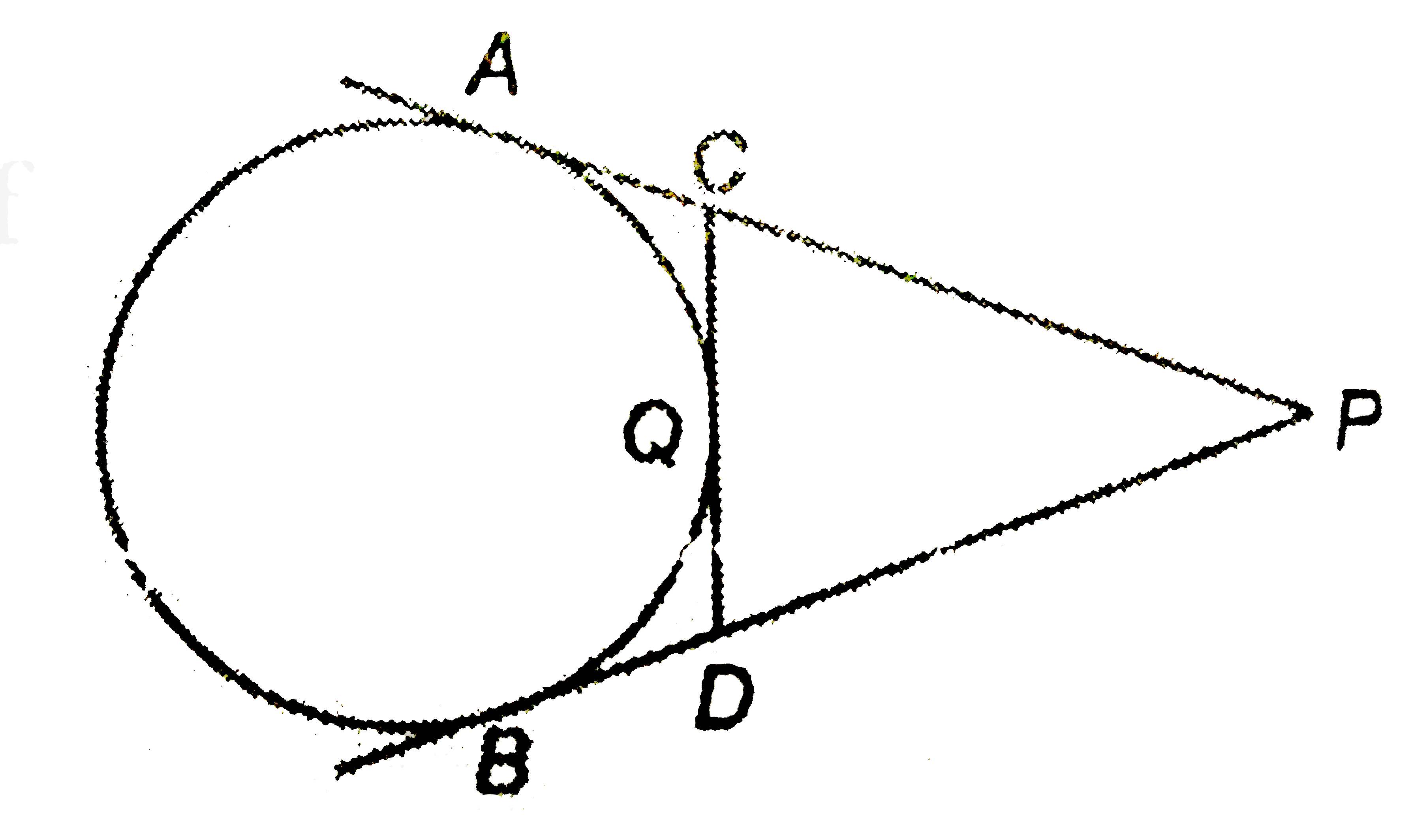
View SolutionIn Fig. 10.74, CP and CQ are tangents to a circle with centre O . ARB is another tangent touching the circle at R . If CP=11cm and BC=7cm , then find the length of BR . (FIGURE)
View SolutionIn Fig. 10.72, PA and PB are tangents to the circle drawn from an external point P . CD is a third tangent touching the circle at Q . If PB=10cm and CQ=2cm , what is the length PC ? (FIGURE)
View SolutionIn the figure, two circles touch each other at the point C.Prove that the common tangents to the circles at C, bisect the common tangents at P and Q.
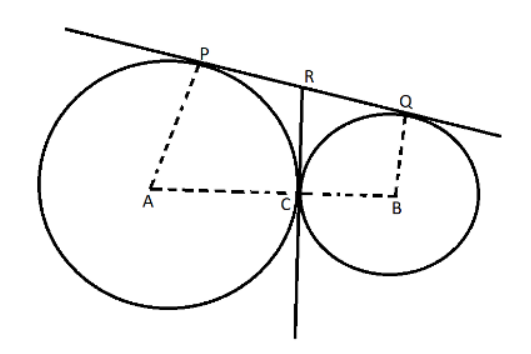
View SolutionIn Figure, two circles touch each other at the point C . Prove that the common tangent to the circles at C , bisects the common tangent at P and Q .
View SolutionA tangent PQ at a point P of a circle of radius 5 cm meets a line through the centre O at a point Q so that OQ=13cm . Find the length of PQ .
View SolutionIn Fig. 10.76, CP and CQ are tangents from an external point C to a circle with centre O . AB is another tangent which touches the circle at R . If CP=11cm and BR=4cm , find the length of BC . (FIGURE)
View SolutionTwo tangents TP and TQ are drawn to a circle with centre O from an external point T . Prove that ∠PTQ=2∠OPQ .
View SolutionTwo tangents TP and TQ are drawn to a circle with centre O from an external point T . Prove that ∠PTQ=2∠OPQ .
View Solution
