Question

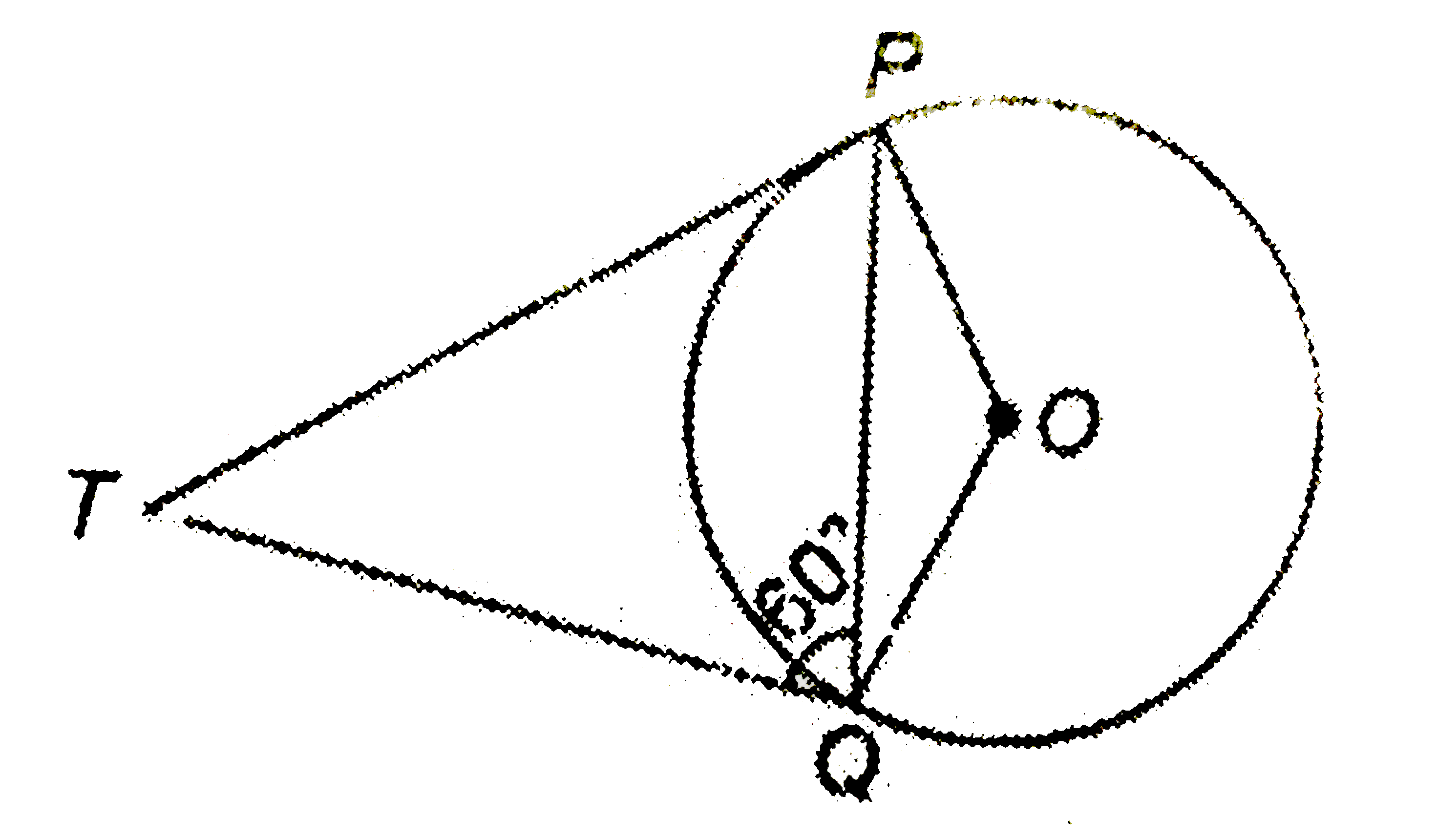
In Fig.
10.96, if $TP$
and $TQ$
are
tangents drawn from an external points $T$
to a circle
with centre $O$
such that $\angle TQP=60o$
, then $\angle OPQ=$
(FIGURE)
$25o$
(b) $30o$
(c) $40o$
(d) $60o$

Explanation

To solve the problem step by step, we will analyze the given information and apply the properties of tangents and triangles.

1. Understanding the Diagram:
- We have a circle with center O.
- Two tangents, TP and TQ, are drawn from an external point T to the circle, touching the circle at points P and Q respectively.
- We know that the angle ∠TQP = 60°.

2. Identifying Properties of Tangents:
- Since TP and TQ are tangents from the same external point T, they are equal in length: TP = TQ.
- The angles formed between the tangent and the radius at the point of tangency are right angles. Therefore, ∠TPO = 90° and ∠TQO = 90°.

3. Analyzing Triangle TPQ:
- Triangle TPQ is isosceles because TP = TQ.
- Since ∠TQP = 60°, the other angle ∠TPQ will also be 60° (because in an isosceles triangle, the angles opposite the equal sides are equal).

4. Calculating the Third Angle in Triangle TPQ:
- The sum of angles in a triangle is 180°. Therefore, we can find the third angle ∠PTQ:
\( \angle PTQ = 180° - \angle TQP - \angle TPQ = 180° - 60° - 60° = 60°. \)

5. Finding Angle OPQ:
- Now, we need to find angle OPQ. We know that:
\( \angle OPQ = \angle TPO - \angle TPQ. \)
- Substituting the known values:
\( \angle OPQ = 90° - 60° = 30°. \)

6. Final Answer:
- Therefore, the angle ∠OPQ is 30°.

Conclusion:
The answer is (b) 30°.

---