The horizontal distance between two poles is 15m. The angle of depression of the top of the first pole as seen from the top of the second pole is 30∘ . If the height of the second pole is 24 m, find the height of the first pole. (√3=1.732)
To solve the problem step by step, we will follow the given information and use trigonometric ratios.
Step 1: Understand the Problem
We have two poles, and we need to find the height of the first pole. The horizontal distance between the two poles is given as 15 m, the height of the second pole is 24 m, and the angle of depression from the top of the second pole to the top of the first pole is 30°.
Step 2: Draw a Diagram
Let’s denote:
- Point A as the top of the first pole.
- Point B as the top of the second pole.
- Point C as the bottom of the first pole.
- Point D as the bottom of the second pole.
The horizontal distance AC = 15 m. The height of the second pole (CD) = 24 m. The angle of depression from B to A is 30°.
Step 3: Set Up the Problem
Let the height of the first pole (CE) be denoted as X. Therefore, the height of the segment DE (the distance from the top of the second pole to the top of the first pole) is:
DE=CD−CE=24−X
Step 4: Use Trigonometric Ratios
In triangle BDE, we can use the tangent of the angle of depression:
tan(30°)=DEBE
Where:
- DE = 24 - X
- BE = AC = 15 m
Now substituting the values:
tan(30°)=24−X15
Step 5: Solve for X
We know that:
tan(30°)=1√3
So we can set up the equation:
1√3=24−X15
Cross-multiplying gives:
15=(24−X)√3
Step 6: Rearranging the Equation
Now, we rearrange the equation to solve for X:
15=24√3−X√3
X√3=24√3−15
X=24√3−15√3
Step 7: Substitute the Value of √3
Given that √3≈1.732:
X=24×1.732−151.732
Calculating the numerator:
24×1.732=41.568
So:
X=41.568−151.732=26.5681.732
Step 8: Final Calculation
Now, calculating the final value:
X≈15.33m
Conclusion
Thus, the height of the first pole is approximately 15.33 meters.
We have two poles, and we need to find the height of the first pole. The horizontal distance between the two poles is given as 15 m, the height of the second pole is 24 m, and the angle of depression from the top of the second pole to the top of the first pole is 30°.
Let’s denote:
- Point A as the top of the first pole.
- Point B as the top of the second pole.
- Point C as the bottom of the first pole.
- Point D as the bottom of the second pole.
Let the height of the first pole (CE) be denoted as X. Therefore, the height of the segment DE (the distance from the top of the second pole to the top of the first pole) is:
DE=CD−CE=24−X
In triangle BDE, we can use the tangent of the angle of depression:
tan(30°)=DEBE
Where:
- DE = 24 - X
- BE = AC = 15 m
tan(30°)=24−X15
We know that:
tan(30°)=1√3
So we can set up the equation:
1√3=24−X15
15=(24−X)√3
Now, we rearrange the equation to solve for X:
15=24√3−X√3
X√3=24√3−15
X=24√3−15√3
Given that √3≈1.732:
X=24×1.732−151.732
24×1.732=41.568
So:
X=41.568−151.732=26.5681.732
Now, calculating the final value:
X≈15.33m
Thus, the height of the first pole is approximately 15.33 meters.
Topper's Solved these Questions
Similar Questions
The horizontal distance between two poles is 15 m. The angle of depression of the top of first pole as seen from the top of second pole is 30°. If the height of the second pole is 24 m, find the height of the first pole. Use v3 =1.732)
View SolutionThe horizontal distance between two towers is 140m. The angle of elevation of the top of the first tower when seen from the top of the second tower is 300. If the height of the second tower is 60m, find the height of the first tower.
View Solution
Knowledge Check
The horizontal distance between two towers is 75 m and the angular depression of the top of the first tower as see from the top of the second, which is 160 m high, is 45∘ . Find the height of the first tower.
A80 mB81 mC85 mDNone
The horizontal distance between two trees of different heights is 60m. The angle of depression of the top of the first tree when seen from the top of the second tree is 45o . If the height of the second tree is 80m, find the height of the first tree.
View SolutionThe horizontal distance between two tower is 150 m. The angle of depression of the top of one tower as observed from the top of other tower, which is 120 m in hight, is 30∘. Find the height of the first tower.
View SolutionThe distance between two towers is 140 m while seeing from the top if the second tower, the angle of elevation of first tower is 30∘.If the height of the second tower is 60 m, then find the height of the first tower.
View SolutionThe horizontal distance between two tower is 120 m. The angle of elevation of the top and angle of depression of the bottom of the first tower as observed from the second tower is 30∘and24∘ respectively.
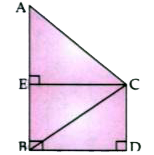
Find the height of the two towers. Give youe answer correct to 3 significant figures.
View SolutionFrom the top of a 50 m high tower, the angles of depression of the top and bottom of a pole are observed to be 45o and 60o respectively. Find the height of the pole.
View SolutionThe angle of elevation of the sun when the length of the shadow of a pole is √3 times the height of the pole is
View SolutionFrom the bottom of a pole of height h, the angle of elevation of the top of a tower is α. The pole subtends an angle β at the top of the tower. find the height of the tower.
View Solution
