A group consists of 12 persons, of which 3 are extremely patient, other 6 are extremely honest and rest are extremely kind. A person from the group is selected at random. Assuming that each person is equally likely to be selected, find the probability of selecting a person who is (i) extremely patient (ii) extremely kind or honest. Which of the above you prefer more.
To solve the problem step by step, we will calculate the probabilities for each scenario as described in the question.
Step 1: Understand the Group Composition
We have a total of 12 persons in the group:
- Extremely Patient: 3 persons
- Extremely Honest: 6 persons
- Extremely Kind: The rest of the persons.
To find the number of extremely kind persons, we subtract the number of extremely patient and extremely honest persons from the total:
Extremely Kind=12−(3+6)=12−9=3
So, there are also 3 extremely kind persons.
Step 2: Calculate the Probability of Selecting an Extremely Patient Person
Let’s denote the event of selecting an extremely patient person as E1.
The probability P(E1) is given by the formula:
P(E1)=Number of favorable outcomesTotal outcomes
Here, the number of favorable outcomes (extremely patient persons) is 3, and the total number of outcomes (total persons) is 12.
Thus, we have:
P(E1)=312=14
Step 3: Calculate the Probability of Selecting an Extremely Kind or Honest Person
Let’s denote the event of selecting an extremely kind or honest person as E2.
To find P(E2), we need to count the number of extremely kind and honest persons:
- Extremely Honest: 6 persons
- Extremely Kind: 3 persons
Total number of favorable outcomes for E2:
Total for E2=6+3=9
Now, we can calculate the probability:
P(E2)=Number of favorable outcomesTotal outcomes=912=34
Step 4: Compare the Probabilities
Now we compare the two probabilities:
- P(E1)=14=0.25
- P(E2)=34=0.75
Since P(E2)>P(E1), we can conclude that selecting a person who is extremely kind or honest is preferred more.
Final Answer
1. The probability of selecting an extremely patient person is 14 or 0.25.
2. The probability of selecting an extremely kind or honest person is 34 or 0.75.
3. Therefore, I prefer selecting a person who is extremely kind or honest more.
We have a total of 12 persons in the group:
- Extremely Patient: 3 persons
- Extremely Honest: 6 persons
- Extremely Kind: The rest of the persons.
Extremely Kind=12−(3+6)=12−9=3
So, there are also 3 extremely kind persons.
Let’s denote the event of selecting an extremely patient person as E1.
P(E1)=Number of favorable outcomesTotal outcomes
Here, the number of favorable outcomes (extremely patient persons) is 3, and the total number of outcomes (total persons) is 12.
P(E1)=312=14
Let’s denote the event of selecting an extremely kind or honest person as E2.
- Extremely Honest: 6 persons
- Extremely Kind: 3 persons
Total for E2=6+3=9
P(E2)=Number of favorable outcomesTotal outcomes=912=34
Now we compare the two probabilities:
- P(E1)=14=0.25
- P(E2)=34=0.75
1. The probability of selecting an extremely patient person is 14 or 0.25.
2. The probability of selecting an extremely kind or honest person is 34 or 0.75.
3. Therefore, I prefer selecting a person who is extremely kind or honest more.
Topper's Solved these Questions
Similar Questions
A group consists of 12 persons, of which 3 are extremely patient, other 6 are extremely honest and rest are extremely kind. A person from the group is selected at random. Assuming that each person is equally likely to be selected, find the probability of selecting a person who is (i) extremely patient (ii) extremely kind or honest. Which of the above values you prefer
View Solutionin submerged hydrophytes,the stems are extremely weak due to
View Solution
Knowledge Check
In simple harmonic motion, at the extreme positions
Akinetic energy is minimum, potential energy is maximumBkinetic energy is maximum, potential energy is minimumCboth kinetic and potential energies are maximum.Dboth kinetic and potential energies are minimumThe bacteria that can survive in extreme salty areas are called
AarchaebacteriaBmethanogensCeubacteriaDhalophiles
There are m persons sitting in a row. Two of the mare selected at random. The probability that the two selected persons are together
View SolutionNuclear waste is an extremely potent pollutant.
View SolutionThe process of industrialization as a whole is extremely hazardous. Comment.
View Solution(n≥5) persons are sitting in a row. Three of these are selected at random. The probability that no two of the selected persons sit together is
View SolutionA recent survey found that the edges ages of workers in a factory as follow.
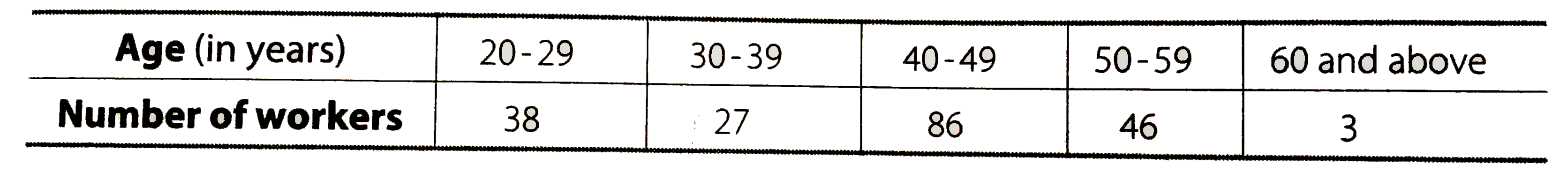
If a person is selected at random, find the probability that the person is
View SolutionBoron has an extremely high melting point because of
View Solution
