Fig. 15.87, shows the cross-section of railway tunnel. The radius OA of the circular part is 2 m. If ∠AOB=90o , calculate: (i) the height of the tunnel (ii) the perimeter of the cross-section (iii) the area of the cross-section.
To solve the problem step by step, we will calculate the height of the tunnel, the perimeter of the cross-section, and the area of the cross-section.
Given:
- Radius OA=2m
- Angle ∠AOB=90∘
Step 1: Calculate the Height of the Tunnel
1. Identify Points: Let O be the center of the circular part, A and B be the points on the circumference, and C and D be the points where the vertical line from O meets AB at right angles.
2. Use Pythagorean Theorem: In triangle AOB, since OA=OB=2m and ∠AOB=90∘:
AB2=OA2+OB2=22+22=4+4=8
AB=√8=2√2m
3. Find AC and BC: Since AC=BC=AB2:
AC=BC=2√22=√2m
4. Calculate OC: In triangle AOC:
OA2=OC2+AC2
22=OC2+(√2)2
4=OC2+2⟹OC2=2⟹OC=√2m
5. Calculate the Height: The height of the tunnel is given by:
Height=OC+OD=√2+2m
Step 2: Calculate the Perimeter of the Cross-section
1. Calculate the Length of the Arc AB: The angle θ for the arc AB is 270∘:
Length of arc=θ360∘×2πR=270360×2π×2
=34×4π=3πm
2. Calculate the Perimeter: The perimeter of the cross-section is:
Perimeter=Length of arc+AB=3π+2√2m
Step 3: Calculate the Area of the Cross-section
1. Calculate the Area of the Sector:
Area of sector=θ360∘×πR2=270360×π×22
=34×4π=3πm2
2. Calculate the Area of Triangle AOB:
Area of triangle=12×OA×OB=12×2×2=2m2
3. Total Area: The area of the cross-section is:
Area=Area of sector+Area of triangle=3π+2m2
Final Answers:
(i) Height of the tunnel: √2+2m
(ii) Perimeter of the cross-section: 3π+2√2m
(iii) Area of the cross-section: 3π+2m2
- Radius OA=2m
- Angle ∠AOB=90∘
2. Use Pythagorean Theorem: In triangle AOB, since OA=OB=2m and ∠AOB=90∘:
AB2=OA2+OB2=22+22=4+4=8
AB=√8=2√2m
3. Find AC and BC: Since AC=BC=AB2:
AC=BC=2√22=√2m
4. Calculate OC: In triangle AOC:
OA2=OC2+AC2
22=OC2+(√2)2
4=OC2+2⟹OC2=2⟹OC=√2m
5. Calculate the Height: The height of the tunnel is given by:
Height=OC+OD=√2+2m
Length of arc=θ360∘×2πR=270360×2π×2
=34×4π=3πm
2. Calculate the Perimeter: The perimeter of the cross-section is:
Perimeter=Length of arc+AB=3π+2√2m
Area of sector=θ360∘×πR2=270360×π×22
=34×4π=3πm2
2. Calculate the Area of Triangle AOB:
Area of triangle=12×OA×OB=12×2×2=2m2
3. Total Area: The area of the cross-section is:
Area=Area of sector+Area of triangle=3π+2m2
(i) Height of the tunnel: √2+2m
Topper's Solved these Questions
Similar Questions
The cross-section of a tunnel is a square of side 7 m surmounted by a semicircle. The tunnel is 80 m long Calculate : the surface area of the tunnel (excluding the floor) .
View SolutionThe cross-section of a tunnel is a square of side 7 m surmounted by a semicircle. The tunnel is 80 m long ,Calculate : its volume
View SolutionThe following figure shows the cross-section ABCD of a swimming pool which is a trapezium in shape.

If the width DC, of the swimming pool is 6.4 m, depth (AD) at the shallow end is 80 cm and depth (BC) at the deepest end is 2.4 m, find its area of cross-section.
View SolutionThe cross-section of a railway tunnel is a square surmounted by a semi-circle as shown in the figure.
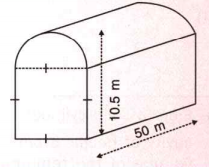
The tunnel is 50 m long. Find the cost of plastering the internal surface of the tunnel (excluding the floor) at the rate of Rs 10 per m2.
View SolutionFind the curved surface area and the total surface area of a right circular cyclinder whose height is 15 cm and the diameter of the cross- sections is 14 cm
View SolutionA uniform current I is flowing in a long wire of radius R. If the current is uniformly distributed across the cross-sectional area of the wire, then
View SolutionIf cross- sectional area of limb I is A1 and that of limb II is A2 then velocity of the liquid in the tube will be, (cross- sectional area of tube is very small)

View SolutionThe cross-section of a railway tunnel is a rectangle 6 m broad and 8 m high surmounted by a semi-circle . The tunnel is 35 m long. Find the cost of plastering the internal surface of the tunnel (excluding the floor) at the rate of Rs 2.25 per m2
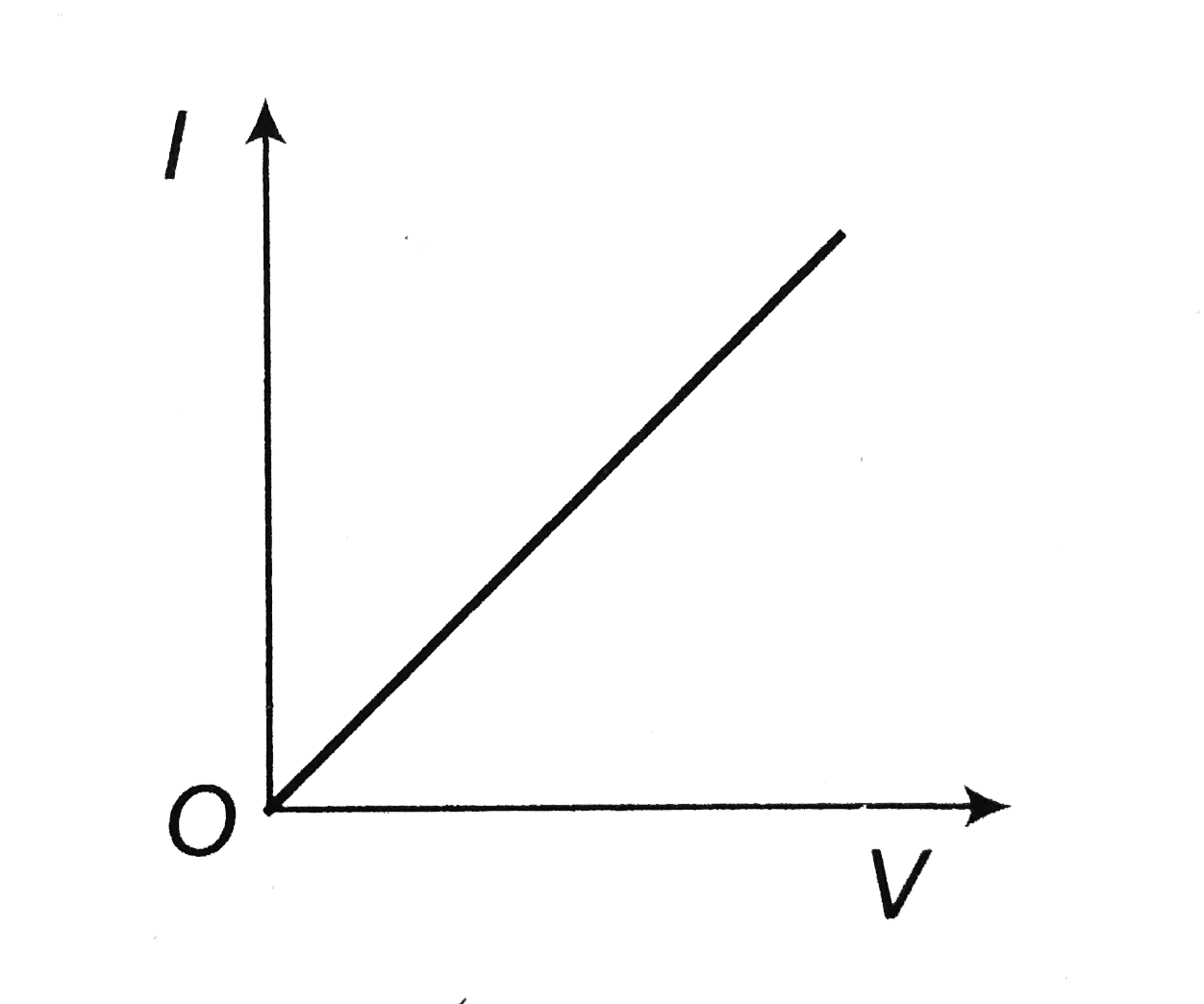
View SolutionI−V characterstic of a copper wire of length L and area fo cross-section A is shown in Fig. The slope of the curve becomes
View SolutionThe pressure exerted on the smaller and the larger piston of a hydraulic machine is 15 Pa Calculate the force exerted by it on the larger piston, if the area of cross section of the larger piston is 4m2.
View Solution
