In Figure, PQ>PR.QS and RS are the bisectors of ∠Q and ∠R respectively. Prove that SQ>SR.
Step by step video & image solution for In Figure, P Q > P R. Q S\ a n d\ R S are the bisectors of /_ Q and /_R respectively. Prove that S Q > S R. by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
In Figure, TQ and TR are the bisectors of ∠Q and ∠R respectively. If ∠QPR=800and ∠PRT=300, determine ∠TQR and ∠QTR
View SolutionIn figure, PQ=PR . Show that PS>PQ.
View SolutionIn ΔPQR, if PQ=QR and L,M and N are the mid-points of the sides PQ,QR and RP respectively. Prove that LN=MN.
View SolutionIn triangle PQR, if PQ=RQ and L, M and N are the mid-points of the sides PQ, QR and RP respectively. Prove that LN=MN.
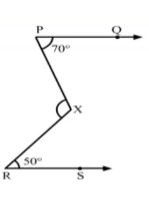
View SolutionIn Figure , find out ∠PXR, if PQ ∣∣ RS.
View SolutionIn Figure, PQRS is a parallelogram. If X and Y are mid-points of PQ and SR respectively and diagonal SQ is joined. The ratio arXQRY: ar (QSR)=
(a) 1:4
(b) 2:1
(c) 1:2
(d) 1:1
View SolutionIn Figure, PQRS is a square. Determine ∠SRP.
View SolutionIn Figure, OP∣∣RS. Determine ∠PQR
View SolutionABCD is a rhombus and P, Q, R, S are the mid-points of AB, BC, CD, DA respectively. Prove that PQRS is a rectangle.
View SolutionIn Figure, ∠PQR= ∠PRQ, then prove that ∠PQS= ∠PRT.
View Solution
