In Figure, TQ and TR are the bisectors of ∠Q and ∠R respectively. If ∠QPR=800and ∠PRT=300, determine ∠TQR and ∠QTR
To solve the problem step by step, we will use the properties of triangles and angle bisectors.
Step 1: Identify the angles in triangle PQR
We know that:
- Angle QPR = 80°
- Angle PRT = 30°
Let’s denote:
- Angle PQR = x
- Angle PRQ = y
According to the triangle angle sum property:
Angle PQR+Angle QPR+Angle PRQ=180°
Thus, we can write:
x+80°+y=180°
This simplifies to:
x+y=100°(Equation 1)
Step 2: Determine angle PRQ
Since TR is the bisector of angle PRQ, we can express angle PRQ in terms of the given angle PRT:
Angle PRQ=Angle PRT+Angle TRQ
This means:
y=30°+Angle TRQ
Step 3: Substitute y in Equation 1
Substituting y in Equation 1:
x+80°+(30°+Angle TRQ)=180°
This simplifies to:
x+110°+Angle TRQ=180°
Thus:
x+Angle TRQ=70°(Equation 2)
Step 4: Find angle PQR
Since TR is the bisector of angle PRQ, we have:
Angle PQR=2×Angle TQR
Let:
Angle TQR=z
Then:
x=2z
Substituting x in Equation 2:
2z+z=70°
This gives:
3z=70°
Thus:
z=70°3=23.33°(approximately 20°)
So:
Angle TQR=20°
Step 5: Find angle QTR
Now we can find angle QTR:
Using the triangle angle sum property in triangle TQR:
Angle TQR+Angle QTR+Angle TRQ=180°
Substituting the known values:
20°+Angle QTR+30°=180°
This simplifies to:
Angle QTR+50°=180°
Thus:
Angle QTR=180°−50°=130°
Final Answers
- Angle TQR = 20°
- Angle QTR = 130°
We know that:
- Angle QPR = 80°
- Angle PRT = 30°
- Angle PQR = x
- Angle PRQ = y
Angle PQR+Angle QPR+Angle PRQ=180°
Thus, we can write:
x+80°+y=180°
This simplifies to:
x+y=100°(Equation 1)
Since TR is the bisector of angle PRQ, we can express angle PRQ in terms of the given angle PRT:
Angle PRQ=Angle PRT+Angle TRQ
This means:
y=30°+Angle TRQ
Substituting y in Equation 1:
x+80°+(30°+Angle TRQ)=180°
This simplifies to:
x+110°+Angle TRQ=180°
Thus:
x+Angle TRQ=70°(Equation 2)
Since TR is the bisector of angle PRQ, we have:
Angle PQR=2×Angle TQR
Let:
Angle TQR=z
Then:
x=2z
Substituting x in Equation 2:
2z+z=70°
This gives:
3z=70°
Thus:
z=70°3=23.33°(approximately 20°)
So:
Angle TQR=20°
Now we can find angle QTR:
Using the triangle angle sum property in triangle TQR:
Angle TQR+Angle QTR+Angle TRQ=180°
Substituting the known values:
20°+Angle QTR+30°=180°
This simplifies to:
Angle QTR+50°=180°
Thus:
Angle QTR=180°−50°=130°
- Angle TQR = 20°
- Angle QTR = 130°
Topper's Solved these Questions
Similar Questions
In Figure, PQ>PR.QS and RS are the bisectors of ∠Q and ∠R respectively. Prove that SQ>SR.
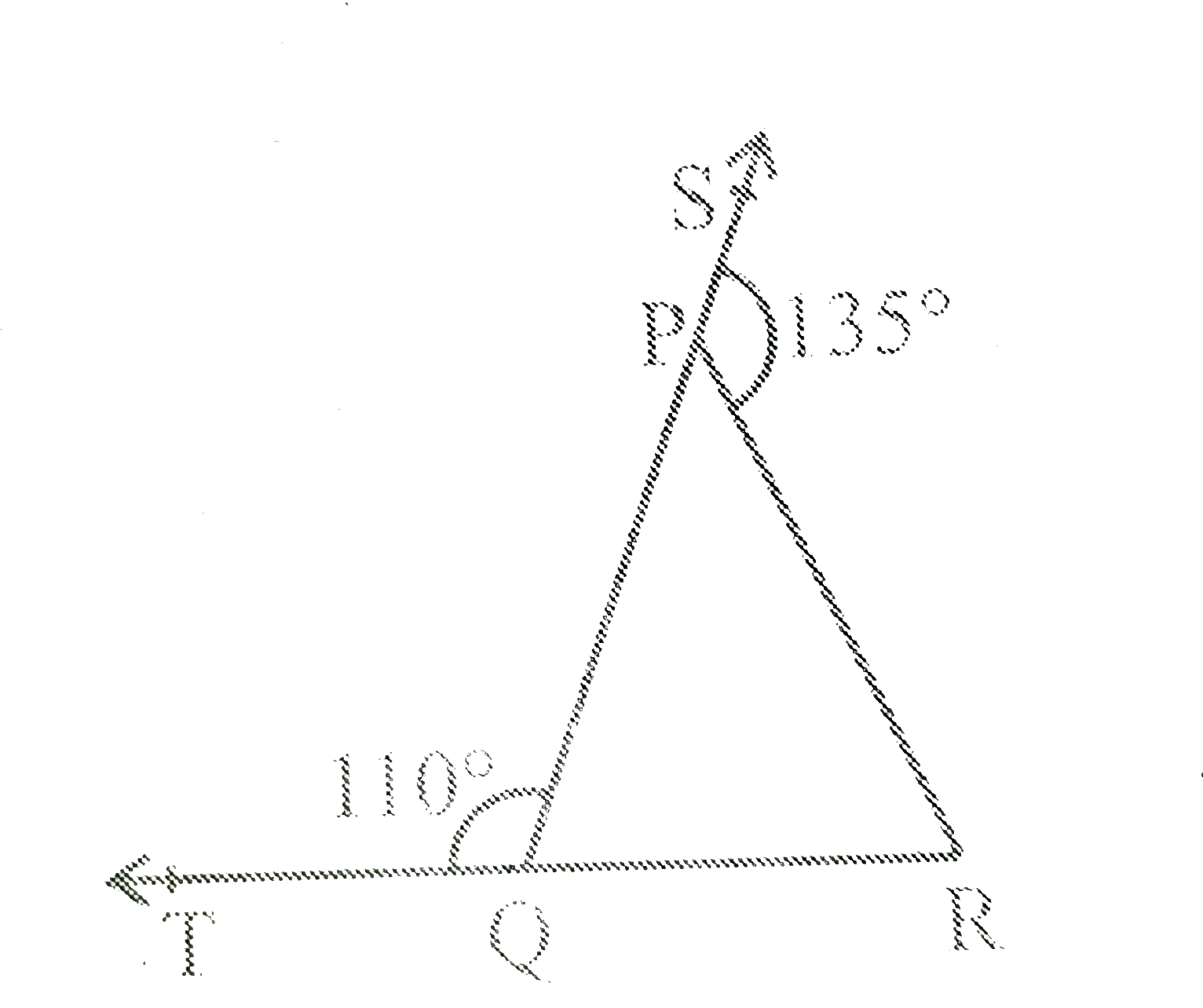
View SolutionIn Figure, side QP and RQ of PQR are produced to point S and T respectively. If ∠SPR=1350and ∠PQT=110∘, find ∠PRQ
View SolutionIn figure, sides QP and RQ of PQR are produced to point S and T respectively. If ∠SPR=1350 and ∠PQT=1100, find ∠PRQ. Figure
View SolutionIn figure, sides QP and RQ of PQR are produced to point S and T respectively. If ∠SPR=1350 and ∠PQT=1100, find ∠PRQ. Figure
View Solutionsides QP and RQ of PQR are produced to point S and T respectively. If ∠SPR=1350 and ∠PQT=1100, find ∠PRQ.
View SolutionIn Fig. 6.39, sides QP and RQ of ΔPQR are produced to point S and T respectively. If ∠SPR=135∘ and ∠PQT=110∘, find ∠PRQ.
View SolutionIn Figure, X and Y are the mid-points of AC and AB respectively, QP∣∣BC and CYQ and BXP are straight lines. Prove that ar ( ABP)= ar ( ACQ).
View SolutionIn Figure, PQRS is a quadrilateral and T and U are respectively points on PS and RS such that PQ=RQ, ∠PQT=∠RQU and ∠TQS=∠UQS. Prove that QT=QU.
View SolutionIn Figure, S and T are points on the sides PQ and PR respectively of △PQR such that PT=2cm , TR=4cm and ST is parallel to QR . Find the ratio of the areas of △PST and △PQR .
View SolutionIn Figure, if QT⊥PR, ∠TQR=40∘ and ∠SPR=30∘, find x and y.
View Solution
