On the sides AB and AC of triangle ABC, equilateral triangles ABD and ACE are drawn. Prove that :
(i) ∠CAD=∠BAE
(ii) CD = BE
Step by step video & image solution for On the sides AB and AC of triangle ABC, equilateral triangles ABD and ACE are drawn. Prove that : (i) angle CAD = angle BAE (ii) CD = BE by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
- TRIANGLES BOOK - ICSECHAPTER - TRIANGLES EXERCISE - QUESTIONS
8 Videos
- TRIANGLES BOOK - ICSECHAPTER - TRIANGLES EXERCISE - 3 MARKS QUESTIONS
11 Videos
- TRIANGLES BOOK - ICSECHAPTER - TRIANGLES EXERCISE - 4 MARKS QUESTIONS
24 Videos
- STATISTICS AND GRAPH WORK BOOK - ICSECHAPTER - STATISTICS AND GRAPH WORK EXERCISE - TOPIC - 2 (4 Marks Questions)
14 Videos
- TRIGONOMETRICAL RATIOS BOOK - ICSECHAPTER - TRIGONOMETRICAL RATIOS EXERCISE - EXERCISE 22(B)
50 Videos
Similar Questions
On the sides AB and AC of triangle ABC, equilateral triangles ABD and ACE are drawn. Prove that :
∠CAD=∠BAE
View SolutionEquilateral triangles ABD and ACE are drawn on sides AB and AC respectively of a ΔABC outside it. Prove that :
(i) ∠DAC=∠EAB (ii) DC=BE
View SolutionThe sides AB and AC of a triangle ABC are produced, and the bisectors of the external angles at B and C meet at P. Prove that if AB>AC, then PC>PB.
View SolutionThe given figure shows a parallelogram ABCD. Squares ABPQ and ADRS are drawn on sides AB and AD of the parallelogram ABCD. Prove that :
(i) ∠SAQ=∠ABC
(ii) SQ = AC

View SolutionIn the following figure, ABC is an equilateral triangle and P is any point in AC, prove that :
(i) BP>PA
(ii) BP>PC
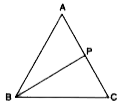
View SolutionIn the following figure, ABC is an equilateral triangle and P is any point in AC, prove that :
(i) BP>PA
(ii) BP>PC

View SolutionThe P lies on side AB of an equilateral triangle ABC. Arrange AC, AP and CP in descending order.
View SolutionAD is a median of triangle ABC. Prove that : AB+AC>2AD
View SolutionThe angles A, B and C of a triangle ABC are in arithmetic progression. AB=6 and BC=7. Then AC is :
View SolutionIn the figure given alongside, squares ABDE and AFGC are drawn on the side AB and the hypotenuse AC of the right triangle ABC.
If BH perpendicular to FG, prove that :
(i) ΔEAC≅ΔBAF.
(ii) Area of the square ABDE
= Area of the rectangle ARHF.
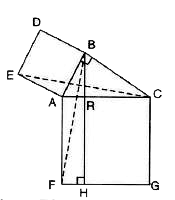
View Solution
