ABCD is a parallelogram. P is the mid-point of AB.BD and CP intersect at Q such that CQ:QP=3:1. If ar (PBQ)=10 cm2, find the area of parallelogram ABCD
Step by step video & image solution for A B C D is a parallelogram. P is the mid-point of A BdotB D\ a n d\ C P intersect at Q such that C Q : Q P=3: 1. If a r\ ( P B Q)=10\ c m^2, find the area of parallelogram A B C D by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
ABCD is a parallelogram. P is a point on AD such that AP=13 AD and Q is a point on BC such that CQ=13BC. Prove that AQCP is a parallelogram.
View SolutionABCD is a parallelogram. P is a point on AD such that AP=13AD and Q is a point on BC such that CQ=13BP . Prove that AQCP is a parallelogram.
View SolutionIn Figure, ABCD is a parallelogram in which P is the mid-point of DC and Q is a point on AC such that CQ=14AC. If PQ produced meets BC at R, prove that R is a mid-point of BC.
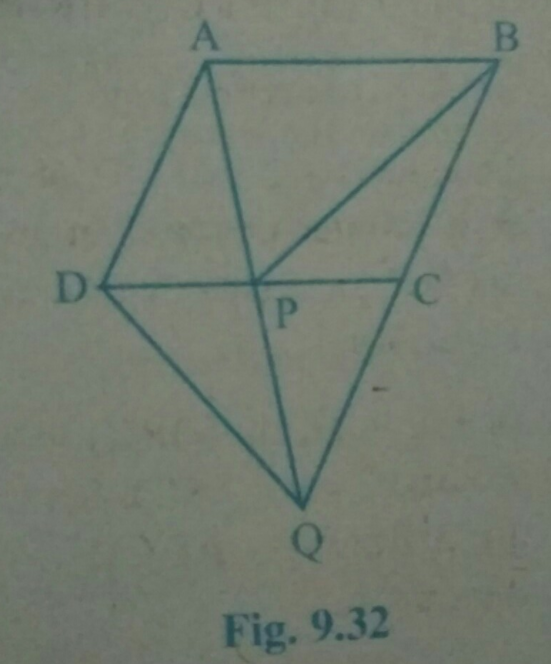
View SolutionIn Fig. 9.32, ABCD is a parallelogram and BC is produced to a point Q such thatAD = CQ. If AQ intersect DC at P, show that ar (BPC) = ar (DPQ).
View SolutionPQRS is a trapezium having PS and QR as parallel sides. A is any point on PQ and B is a point on SR such that AB∣∣QR . If area of △PBQ is 17 cm2, find the area of △ASR
View SolutionABCD is a parallelogram whose diagonals AC and BD intersect at O. A Line through O intersects AB at P and DC at Q. Prove that ar(POA)=ar(QOC).
View SolutionIn Figure, ABCD is a parallelogram in which P is the mid-point of DC and Q is a point on AC such that CQ=14AC. If PQ produced meets BC at R. Prove that R is a mid-point of BC.
View SolutionABCD is a parallelogram. A circle through A, B is so drawn that it intersects AD at P and BC at Q. Prove that P, Q, C and D are concyclic.
View SolutionABCD is a parallelogram, E and F are the mid-points of AB and CD respectively. GH is any line intersecting AD, EF and BC at G, P and H respectively. Prove that GP=PH
View SolutionIn ABC,D is the mid-point of AB,P is any point of BC.CQPD meets AB in Q . Show that ar(BPQ)=12ar(ABC).
View Solution