The side AB of a parallelogram ABCD is produced to any point P. A line through A and parallel to CP meets CB produced at Q and then parallelogram PBQR is completed as shown in Figure. Show that ar(∣∣gmABCD)=ar(∣∣gmPBQR)
Step by step video & image solution for The side AB of a parallelogram ABCD is produced to any point P. A line through A and parallel to CP meets CB produced at Q and then parallelogram PBQR is completed as shown in Figure. Show that ar(||^(gm) ABCD)=ar (||^(gm) PBQR) by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
The side AB of a parallelogram ABCD is produced to any point P. A line through A and parallel to CP meets CB produced at Q and then parallelogram PBQR is completed as shown in Figure. Show that ar(^(gm)ABCD)=argmPBQR).
View SolutionThe side AB of a parallelogram ABCD is produced to any point P. A line through A and parallel to CP meets CB produced at Q and then parallelogram PBQR is completed. Show that ar (ABCD) = ar (PBQR).
View SolutionThe side AB of a parallelogram ABCD is produced to any point P. A line through A parallel to CP meets CB produced in Q and the parallelogram PBQR completed. Show that ar(^(gm)ABCD)=ar(^(gm)BPRQ). CONSTRUCTION : Join AC and PQ. TO PROVE : ar(^(gm)ABCD)=ar(^(gm)BPRQ)
View SolutionThe side AB of a parallelogram ABCD is produced to any point P. A line through A parallel to CP meets CB produced in Q and the parallelogram PBQR completed. Show that ar(llgmABCD)=ar(llgmBPRQ). CONSTRUCTION : Join AC and PQ. TO PROVE : ar(llgmABCD)=ar(llgmBPRQ)
View SolutionIn parallelogram ABCD, E is mid-point of CD and through D, a line is drawn parallel to EB to meet CB produced at point G and to cut AB at point F. Prove that :
DG = 2EB
View SolutionIn parallelogram ABCD, E is mid-point of CD and through D, a line is drawr parallel to EB to meet CB produced at point G and to cut AB at point F. Prove that:
2×AD=GC
View SolutionIn triangle ABC, P is the mid-point of side BC. A line through P and parallel to CA meets AB at point Q and a line through Q and parallel to BC meets median AP at point R. Prove that :
AP=2AR
View SolutionIn parallelogram ABCD, E is the mid-point of AB and AP is parallel to EC which meets DC at point O and BC produced at P. Prove that:
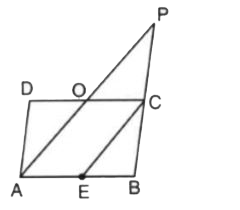
PB=2AD
View SolutionIn figure, ABCDE is any pentagon. BP drawn parallel to AC meets DC produced at P and EQ drawn parallel to AD meets CD produced at Q. Prove that ar(ABCDE)=ar(ΔAPQ).
View SolutionIn the parallelogram ABCD , the side AB is produced to the point X.so that BX= AB. The line DX cuts BC at E. Prove that :
DBXC is a parallelogram.
View Solution
