In figure, ABCDE is any pentagon. BP drawn parallel to AC meets DC produced at P and EQ drawn parallel to AD meets CD produced at Q. Prove that ar(ABCDE)=ar(ΔAPQ).
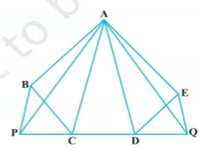
Given ABCDE is a pentagon.
BP∣∣AC and EQ∣∣AD.
To prove ar(ABCDE)=ar(APQ)
Proof We know that, triangles on the same base and between the same parallels are equal in area.
Here, ΔADQ and ΔADE lie on the same base AD and between the same parallels AD and EQ.
So, ar(ΔADQ)=ar(ΔADE) ...(i)
Similarly, ΔACP and ΔACB lie on the same base AC and between the same parallels AC and BP.
So, ar(ΔACP)=ar(ΔACB) ...(ii)
On adding Eqs. (i) and (ii), we get
ar(ΔADQ)+ar(ΔACP)=ar(ΔADE)+ar(ΔACB)
On adding ar(ΔACD) both sides, we get
ar(ΔADQ)+ar(ΔACP)+ar(ΔACD)=ar(ΔADE)+ar(ΔACB)+ar(ΔACD)
⇒ ar(ΔAPQ)=ar(ABCDE) Hence proved.
Topper's Solved these Questions
Similar Questions
The given figure shows a pentagon ABCDE. EG drawn parallel to DA meets BA produced at G and CF drawn parallel to DB meets AB produced at F.
Prove that the area of pentagon ABCDE is equal to the area of triangle GDF.
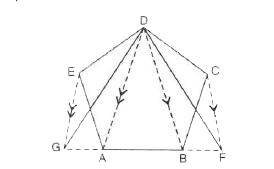
View SolutionThe given figure shows a pentagon ABCDE. EG drawn parallel to DA meets BA produced at G and CF drawn parallel to DB meets AB produced at F.
Prove that the area of pentagon ABCDE is equal to the area of triangle GDF.

View SolutionIn the given figure, ABCD is a parallelogram. AB is produced to P, such that AB=BPandPQ is drawn parallel to BC to meet AC produced at Q. Given AB=8cm,AD=5cm,AC=10cm.
Prove that point C is mid-point of AQ.
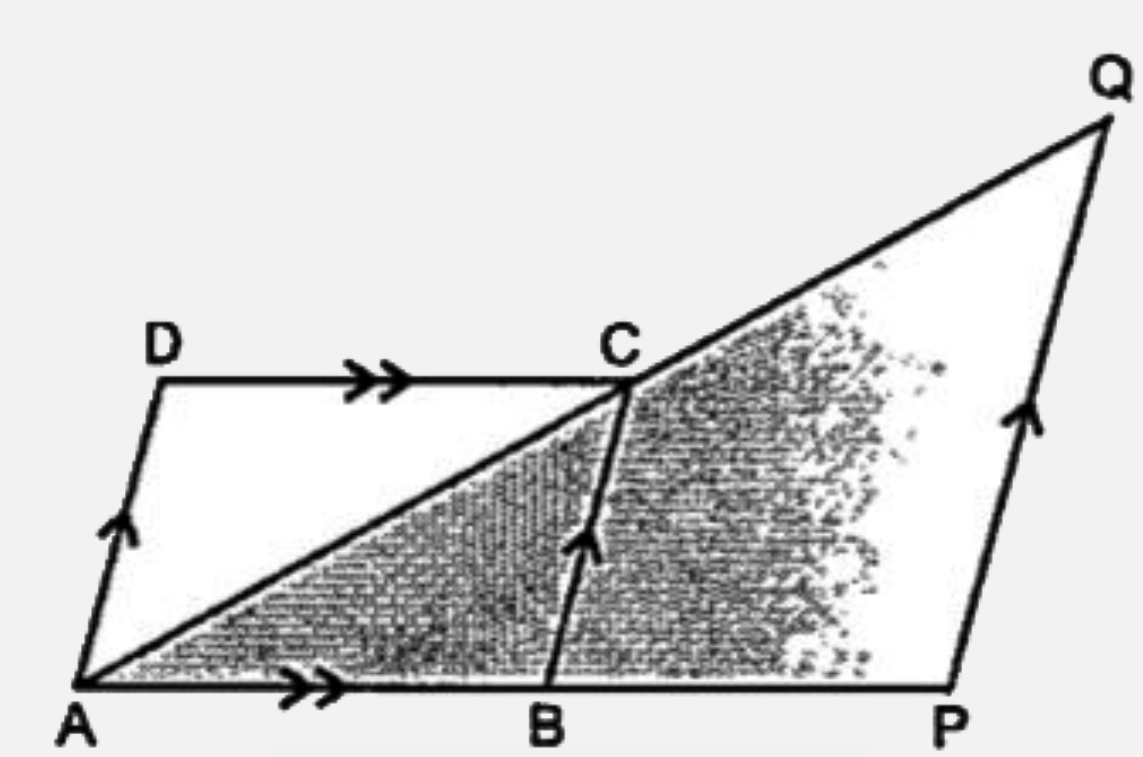
View SolutionIn the given figure, ABCD is a parallelogram. AB is produced to P, such that AB=BPandPQ is drawn parallel to BC to meet AC produced at Q. Given AB=8cm,AD=5cm,AC=10cm.
Find the perimeter of quadrilateral BCQP.

View SolutionThe side AB of a parallelogram ABCD is produced to any point P. A line through A and parallel to CP meets CB produced at Q and then parallelogram PBQR is completed. Show that ar (ABCD) = ar (PBQR).
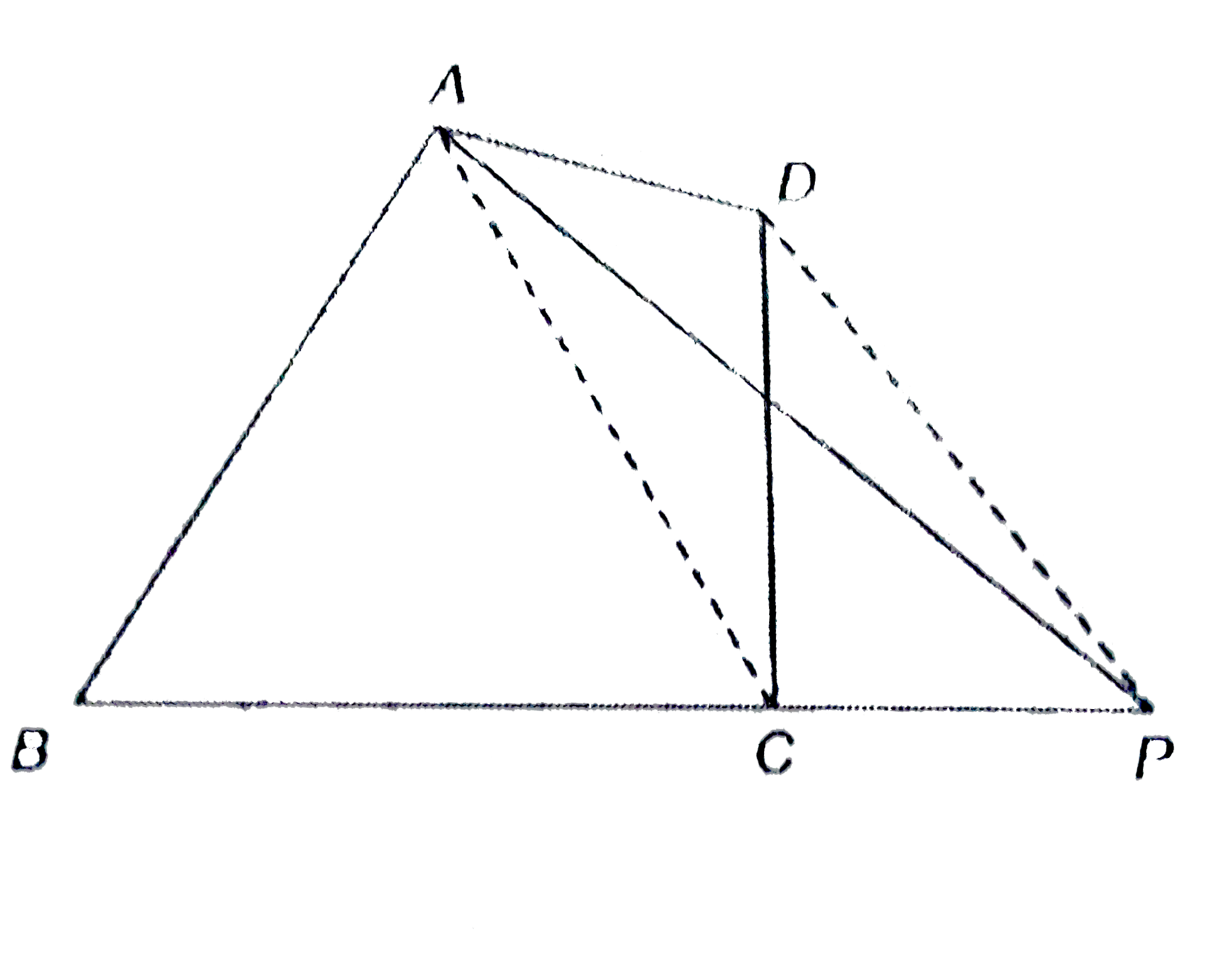
View SolutionIn the figure, ABCD is a quadrilateral. A line DP drawn parallel to diagonal AC from point D, meet BC produced at P. Prove that:
are of ΔABP= area of □ABCD
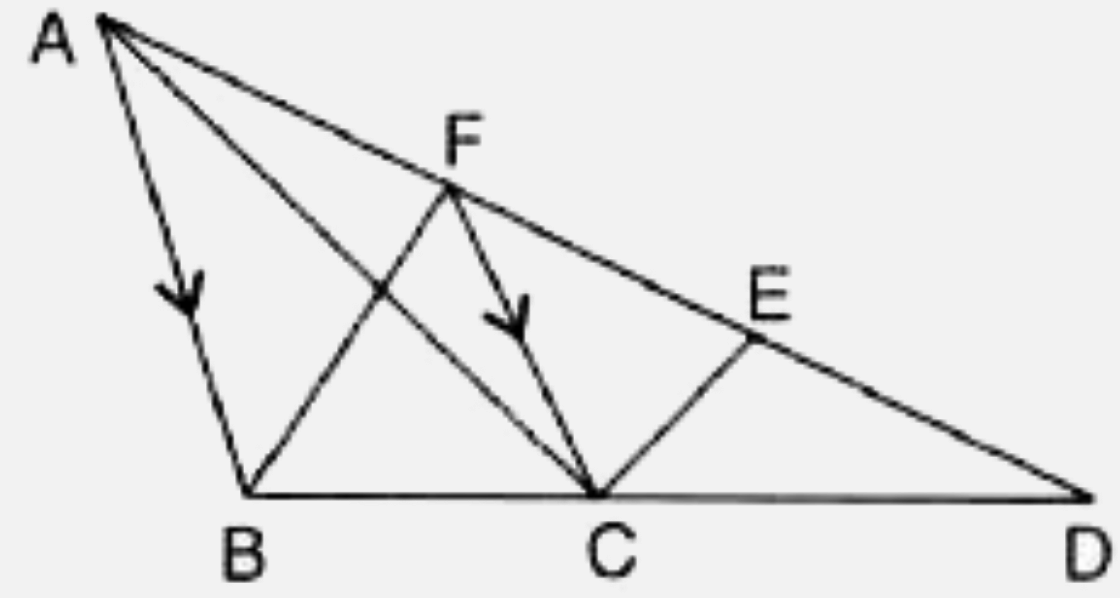
View SolutionIn the following figure, F and E are points on the side AD of the triangle ABD. Through F a line is drawn parallel to AB to meet BD at point C .
Prove that : ar (ΔACE)=ar (quad . BCEF )
View SolutionIn parallelogram PQRS. L is mid-point of side Sr and SN is drawn parallel to LQ which meets RQ produced prove that :
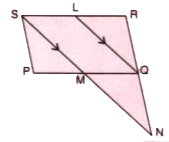
SN=2LQ
View SolutionThe side AB of a parallelogram ABCD is produced to any point P. A line through A and parallel to CP meets CB produced at Q and then parallelogram PBQR is completed as shown in Figure. Show that ar(∣∣gmABCD)=ar(∣∣gmPBQR)
View SolutionIn parallelogram ABCD, E is the mid-point of AB and AP is parallel to EC which meets DC at point O and BC produced at P. Prove that :
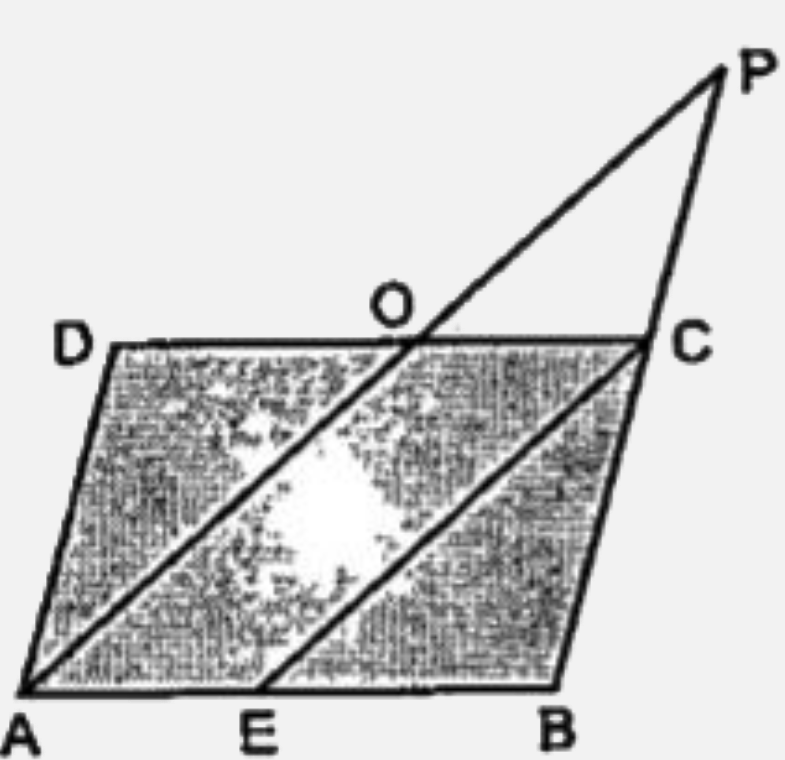
BP=2AD
View Solution
