A circular park of radius 20m is situated in a colony. Three boys Ankur, Syed and David are sitting at equal distance on its boundary each having a toy telephone in his hands to talk to each other. Find the length of the string of each phone.
To solve the problem, we need to find the length of the string of each toy telephone held by the boys Ankur, Syed, and David, who are sitting at equal distances on the boundary of a circular park with a radius of 20 meters.
1. Understanding the Setup:
- The boys are sitting at equal distances on the boundary of a circular park, which implies that they form an equilateral triangle.
- Let the radius of the circular park be R=20 meters.
2. Labeling the Points:
- Let the positions of the boys be represented as points A, S, and D.
- The distance between any two boys (the side of the equilateral triangle) is denoted as x.
3. Dropping a Perpendicular:
- Drop a perpendicular from the center of the circle O to the midpoint B of side SD of the triangle ASD.
- This creates two right triangles: △ABS and △ABD.
4. Using the Properties of the Triangle:
- Since B is the midpoint, we have SB=BD=x2.
- The height AB can be calculated using the Pythagorean theorem in triangle ABS.
5. Applying Pythagorean Theorem:
- In triangle ABS:
AS2=AB2+BS2
Here, AS=x (the side of the triangle), BS=x2, and AB is the height.
x2=AB2+(x2)2
x2=AB2+x24
Rearranging gives:
AB2=x2−x24=3x24
Taking the square root:
AB=√3x2
6. Finding the Length of OB:
- The length OB can be expressed as:
OB=OA−AB
where OA=20 meters (the radius).
OB=20−√3x2
7. Using the Right Triangle OBS:
- In triangle OBS:
OS2=OB2+SB2
Here, OS=20, SB=x2:
202=(20−√3x2)2+(x2)2
Expanding and simplifying:
400=(20−√3x2)2+x24
400=400−20√3x+3x24+x24
0=−20√3x+x2
Rearranging gives:
x2=20√3x
Dividing by x (assuming x≠0):
x=20√3 meters
Final Answer:
The length of the string of each toy telephone is 20√3 meters.
---
- The boys are sitting at equal distances on the boundary of a circular park, which implies that they form an equilateral triangle.
- Let the radius of the circular park be R=20 meters.
- Let the positions of the boys be represented as points A, S, and D.
- The distance between any two boys (the side of the equilateral triangle) is denoted as x.
- Drop a perpendicular from the center of the circle O to the midpoint B of side SD of the triangle ASD.
- This creates two right triangles: △ABS and △ABD.
- Since B is the midpoint, we have SB=BD=x2.
- The height AB can be calculated using the Pythagorean theorem in triangle ABS.
- In triangle ABS:
AS2=AB2+BS2
Here, AS=x (the side of the triangle), BS=x2, and AB is the height.
x2=AB2+(x2)2
x2=AB2+x24
Rearranging gives:
AB2=x2−x24=3x24
Taking the square root:
AB=√3x2
- The length OB can be expressed as:
OB=OA−AB
where OA=20 meters (the radius).
OB=20−√3x2
- In triangle OBS:
OS2=OB2+SB2
Here, OS=20, SB=x2:
202=(20−√3x2)2+(x2)2
Expanding and simplifying:
400=(20−√3x2)2+x24
400=400−20√3x+3x24+x24
0=−20√3x+x2
Rearranging gives:
x2=20√3x
Dividing by x (assuming x≠0):
x=20√3 meters
The length of the string of each toy telephone is 20√3 meters.
Topper's Solved these Questions
Similar Questions
A circular park of radius 20m is situated in a colony. Three boys Ankur, Syed and David are sitting at equal distance on its boundary each having a toy telephone in his hands to talk each other. Find the length of the string of each phone.
View SolutionA circular park of radius 20m is situated in a colony. Three boys Ankur, Syed andDavid are sitting at equal distance on its boundary each having a toy telephone inhis hands to talk each other. Find the length of the string of each phone.
View SolutionThree girls skating on a circular ice ground of radius 200m start from a point (P) on the edge of the ground and reach a point Q diametrically opposite to (P) following different paths as shown in Fig. What is the magnitude of the displacement vector for each ? which girl's displacement is equal to the actual length of path skate ?
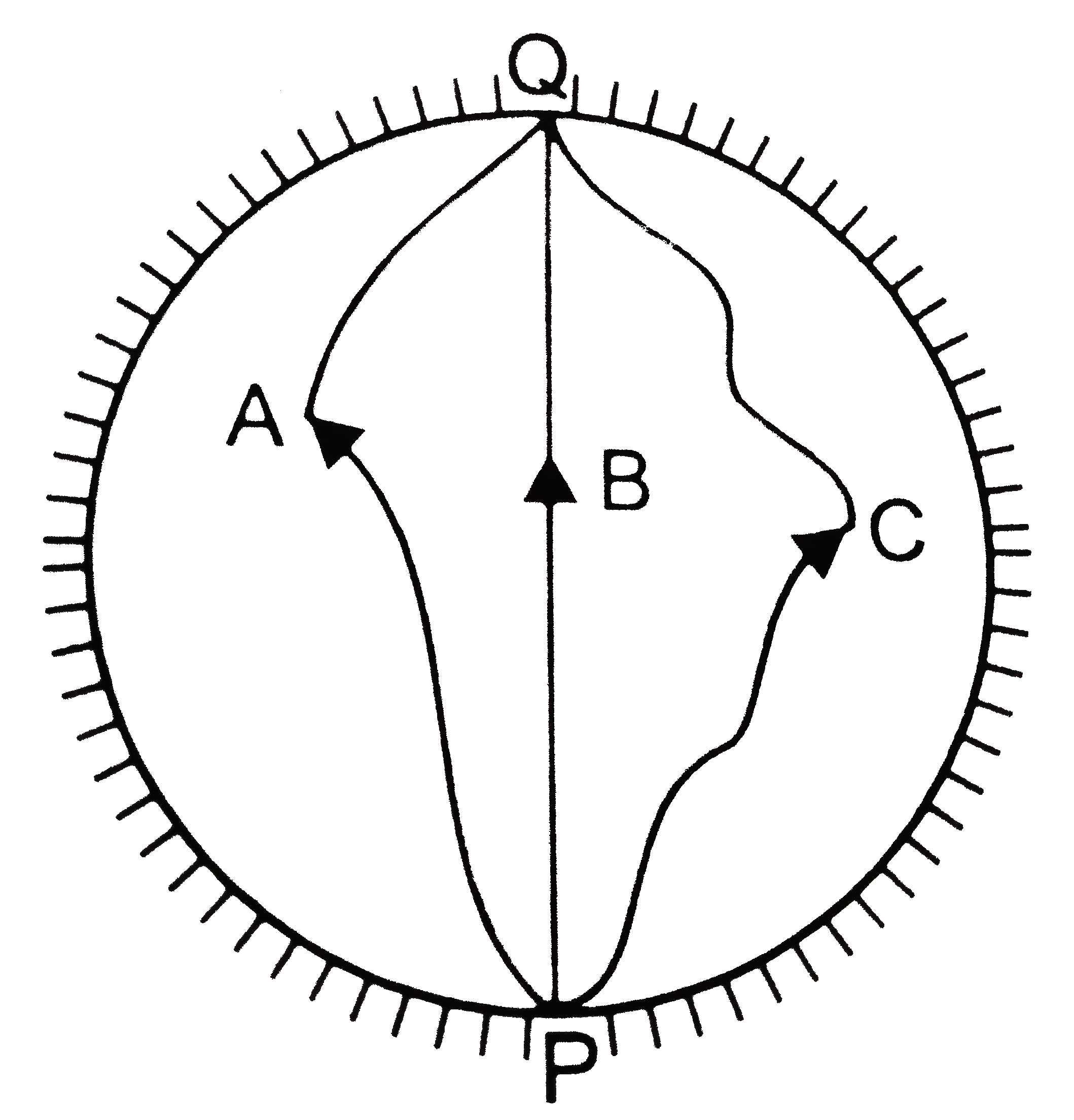 .
.
View SolutionA uniform thin cylindrical disk of mass M and radius R is attaached to two identical massless springs of spring constatn k which are fixed to the wall as shown in the figure. The springs are attached to the axle of the disk symmetrically on either side at a distance d from its centre. The axle is massless and both the springs and the axle are in horizontal plane. the unstretched length of each spring is L. The disk is initially at its equilibrium position with its centre of mass (CM) at a distance L from the wall. The disk rolls without slipping with velocity →V0=vacV0ˆi. The coefficinet of friction is μ.
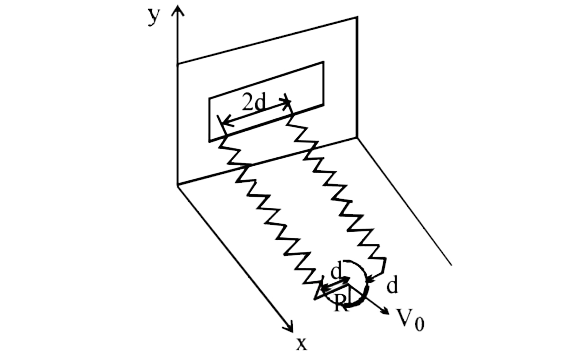
The centre of mass of the disk undergoes simple harmonic motion with angular frequency ω equal to -
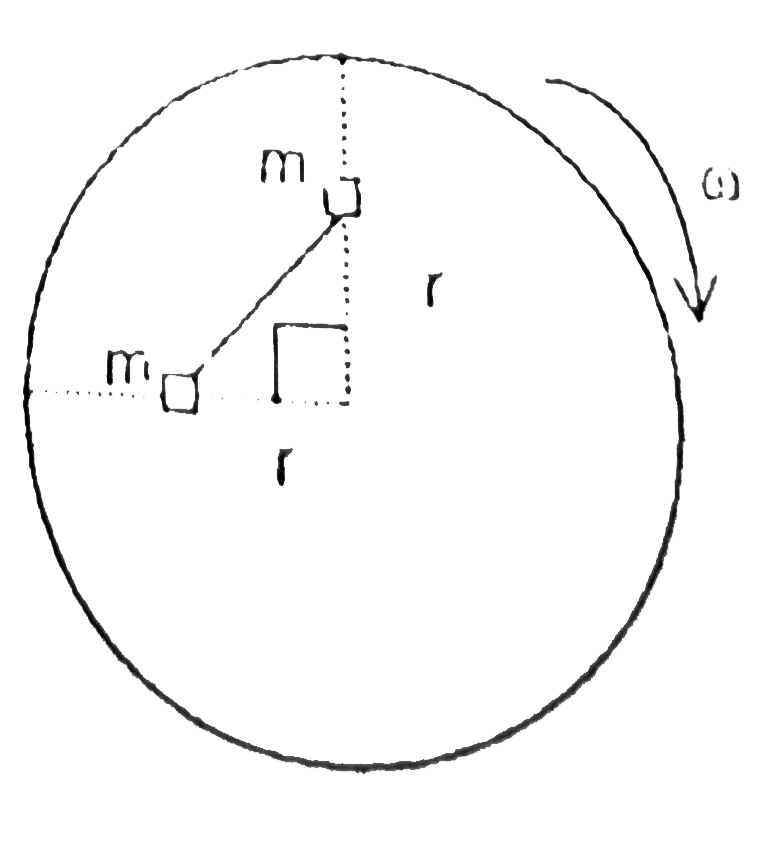
View SolutionTwo particles of mass m each are kept on a horizontal circular platfrom on two mutually perpendicular radii at equal distance r from the center of the table. The particles are connected with a string, which is just taught when the platfrom is not rotating. The coefficient of static friction between the platfrom and block is μ (now if angular speed of platfrom m is slowly increased). Find the maximum angular speed (ω) of platfrom about it center so that the blocks remain stationery relative to platform. (If μ=1√2, r=2.5m and g=10m/s2)
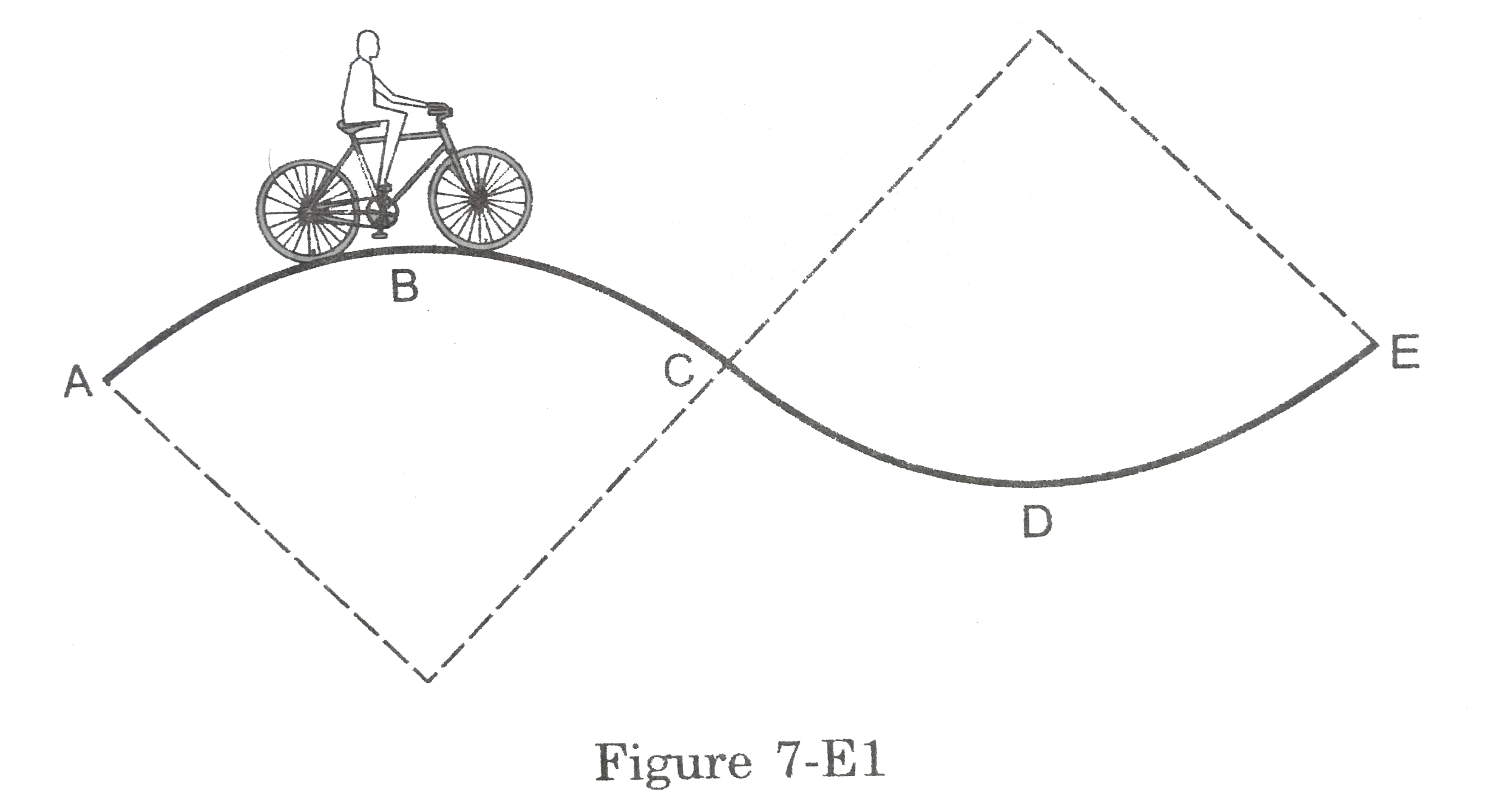
View SolutionA track consists of two circular pars ABC and CDE of equal radius 100 m and joined smoothly as shown in figure.Each part subtends a right angle at its centre. A cycle weighing 100 kg together with rider travels at a constant speed of 18 km/h on the track. A. Find the normal contact force by the road on the cycle when it is at B and at D. b.Find the force of friction exerted by the track on the tyres when the cycle is at B,C and D. c. Find the normal force between the road and the cycle just before and just after the cycle crosses C. d. What should be the minimum friction coefficient between the road and the tyre, which will ensure that the cyclist can move with constant speed? Take g=10ms2
View SolutionConsider a point charge q=1mC placed at a corner of a cube of sides 10 cm . Determine the electric flux through each face of the cube.
Strategy : We will learn about the utility of symmetry in solving problems with the help of Gauss's law . Here we'll use the symmetry of the situation,which involves the faces joining at the corner at which the charge resides.

(a) A charge q is placed atthe corner of a cube. (b) By surrounding the charge with a series of cubes such that the charge is at the centre of a larger cube, we have created an arrangement sufficiently symmetric to be able to solve for desired flux values.
You can see from figure that for these faces →E.ˆn=0. Since the normal is perpendicular to the surfaces while the electric field goes off in a spherically symmetric pattern and lies in the sides . In other words , the electric field that originates at the charge is tangential to the surface of these three sides. This means there is no flux through these sides. The electric flux through each of the remaining three faces of the be must be equal by symmetry . We'll referto these faces with the label F.
To fidn the flux through each of the sides F, we acan use a technique that puts the single charge in the middle of a larger cube. It takes seven other similarly placed cubes to surrounds the points charge q completely in figre. The charge is at the dead centre of the enw larger cube. So, the flux through each of the six sides of the large cube will now have an electric flux of one sixth of the total flux F. So given that the total structure is completely symmetric, the flux through a side F is one fourth of the flux through the larger side.
View SolutionThree uniform spheres each having a mass M and radius a are kept in such a way that each touches the other two. Find the magnitude of the gravitational force on any of the spheres due to the other two.
View SolutionThree uniform spheres each having a mass M and radius a are kept in such a way that each touches the other two. Find the magnitude of the gravitational force on any of the spheres due to the other two.
View SolutionThree uniform spheres each having a mass M and radius a are kept in such a way that each touches the other two. Find the magnitude of the gravitational force on any of the spheres due to the other two.
View Solution