A circular park of radius 20m is situated in a colony. Three boys Ankur, Syed andDavid are sitting at equal distance on its boundary each having a toy telephone inhis hands to talk each other. Find the length of the string of each phone.
The positions of Ankur, Syed and David are represented as A, B and C respectively.
As they are sitting at equal distances, then triangle is equilateral.
AD is the median of △ABC and it passes through the centre O.
O is the centroid of the △ABC. OA is the radius of the triangle.
OA=23AD
Let the side of a triangle a metres then
BD=a2
Apply Pythagoras Theorem in △ABD.
AB2=BD2+AD2
AD2=AB2−BD2
AD2=a2−(a2)2
AD2=3a24
AD=√3a2
Thus, substitute the value of OA as 20 and evaluate.
20=23×√3a2
a=20√3
The length of the string of the toy is 20√3m.
Similar Questions
A circular park of radius 20m is situated in a colony. Three boys Ankur, Syed and David are sitting at equal distance on its boundary each having a toy telephone in his hands to talk each other. Find the length of the string of each phone.
View SolutionA circular park of radius 20m is situated in a colony. Three boys Ankur, Syed and David are sitting at equal distance on its boundary each having a toy telephone in his hands to talk to each other. Find the length of the string of each phone.
View SolutionA circular park of radius 20m is situated in a colony. Three boys Ankur, Syed and David are sitting at equal distance on its boundary each having a toy telephone in his hands to talk to each other. Find the length of the string of each phone.
View SolutionThree girls skating on a circular ice ground of radius 200m start from a point (P) on the edge of the ground and reach a point Q diametrically opposite to (P) following different paths as shown in Fig. What is the magnitude of the displacement vector for each ? which girl's displacement is equal to the actual length of path skate ?
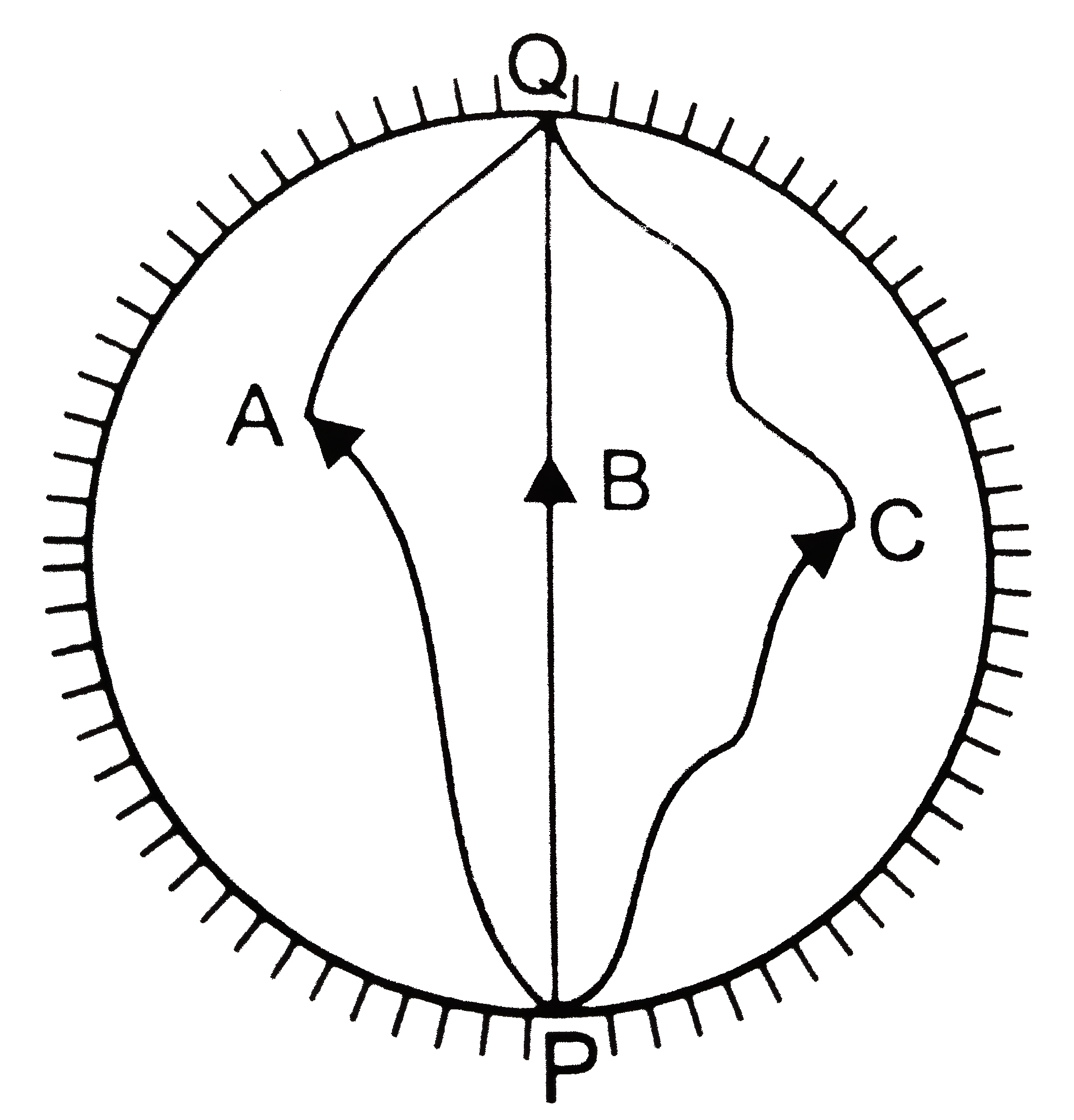 .
.
View SolutionA uniform bar of length 12L and mass 48m is supported horizontally on two fixed smooth tables as shown in figure. A small moth (an insect) of mass 8m is sitting on end A of the rod and a spider (an insect) of mass 16m is sitting on the other end B. Both the insects moving towards each other along the rod with moth moving at speed 2v and the spider at half this speed (absolute). They meet at a point P on the rod and the spider eats the moth. After this the spider moves with a velocity v2 relative to the rod towards the end A. The spider takes negligible time in eating on the other insect. Also, let v=LT where T is a constant having value 4s.
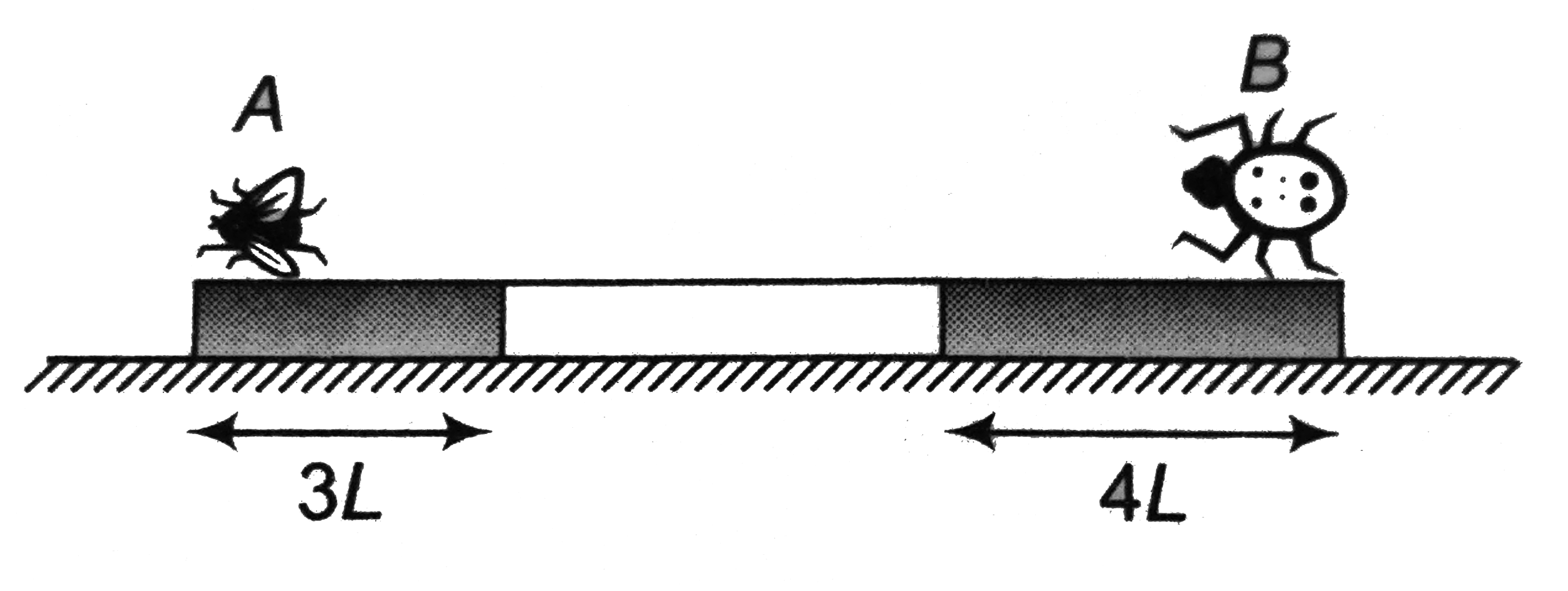
By what distance the centre of mass of the rod shifts during this time?
View SolutionA uniform thin cylindrical disk of mass M and radius R is attaached to two identical massless springs of spring constatn k which are fixed to the wall as shown in the figure. The springs are attached to the axle of the disk symmetrically on either side at a distance d from its centre. The axle is massless and both the springs and the axle are in horizontal plane. the unstretched length of each spring is L. The disk is initially at its equilibrium position with its centre of mass (CM) at a distance L from the wall. The disk rolls without slipping with velocity →V0=vacV0ˆi. The coefficinet of friction is μ.
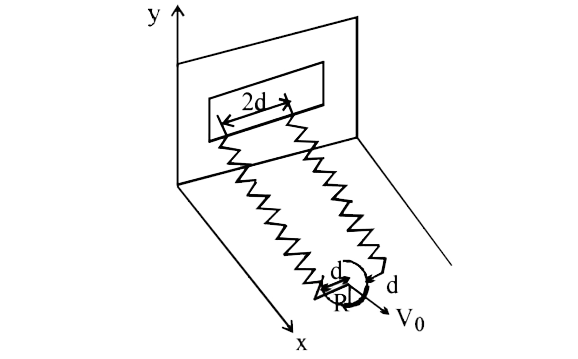
The centre of mass of the disk undergoes simple harmonic motion with angular frequency ω equal to -
View SolutionA charged ball of mass 5.88×10−4 kg is suspended from two silk strings of equal lengths so that the strings are inclined at 60∘ with each other. Another ball carrying a charge which is equal in magnitude but opposite in sign of the first one is placed vertically below the first one at a distance of 4.2×10−2m. Due to this, the tension in the strings is doubled. Determine the charge on the ball and the tension in the strings after electrostatic interaction. (g=9.8m/s2)
View SolutionTwo particles of mass M=3kg each are kept on a horizontal circular platform on two mutually perpendicular radii at equal distance R=1m from the centre of the table. The particles are connected with a string,which is just taught when the platform is not rotating.Coefficient of friction between the platform and block is μ=0.4.Then the maximum angular speed (ω in radsec) of platform about its centre so that the blocks remain stationary relative to platform is (take g=10.ms2 )
View SolutionTwo particles of mass m each are kept on a horizontal circular platfrom on two mutually perpendicular radii at equal distance r from the center of the table. The particles are connected with a string, which is just taught when the platfrom is not rotating. The coefficient of static friction between the platfrom and block is μ (now if angular speed of platfrom m is slowly increased). Find the maximum angular speed (ω) of platfrom about it center so that the blocks remain stationery relative to platform. (If μ=1√2, r=2.5m and g=10m/s2)
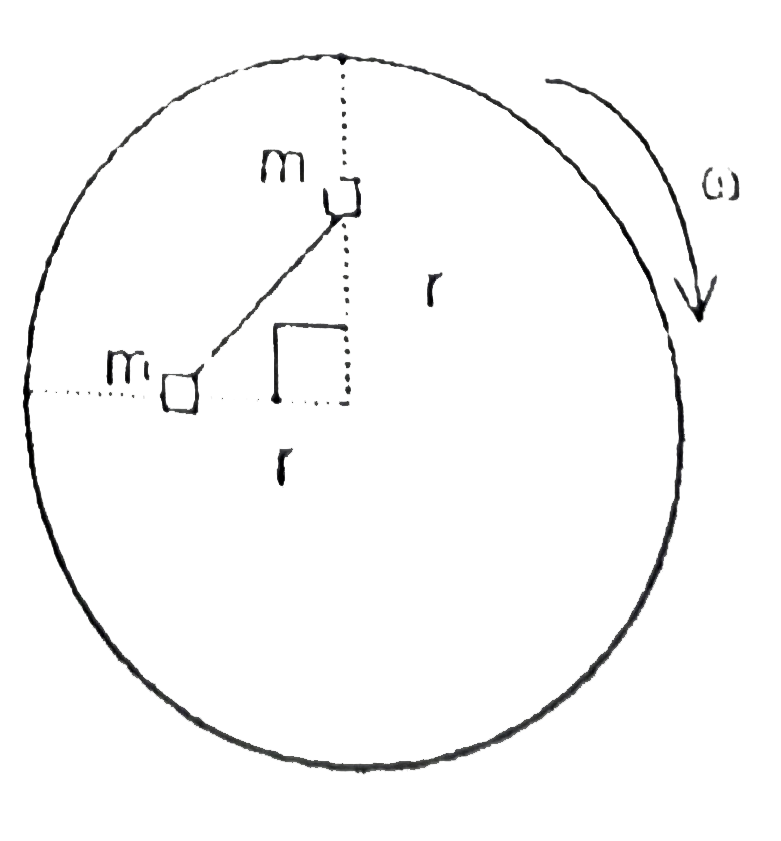
View SolutionA track consists of two circular pars ABC and CDE of equal radius 100 m and joined smoothly as shown in figure.Each part subtends a right angle at its centre. A cycle weighing 100 kg together with rider travels at a constant speed of 18 km/h on the track. A. Find the normal contact force by the road on the cycle when it is at B and at D. b.Find the force of friction exerted by the track on the tyres when the cycle is at B,C and D. c. Find the normal force between the road and the cycle just before and just after the cycle crosses C. d. What should be the minimum friction coefficient between the road and the tyre, which will ensure that the cyclist can move with constant speed? Take g=10ms2

View Solution